এক্সেল এ লিনিয়ার প্রোগ্রামিং কিভাবে গ্রাফ করবেন (বিস্তারিত ধাপ সহ)

অনেক সময় লিনিয়ার প্রোগ্রামিং এর মাধ্যমে আমাদের একাধিক ভেরিয়েবল সমাধান করতে হয়। লিনিয়ার প্রোগ্রামিং সমাধানের বিভিন্ন উপায় রয়েছে। লিনিয়ার প্রোগ্রামিং সমাধানের সবচেয়ে সহজ পদ্ধতি হল গ্রাফিং। এই নিবন্ধে, আমি আপনাকে এক্সেলে রৈখিক প্রোগ্রামিং গ্রাফ করার বিস্তারিত পদক্ষেপ দেখাব।

আপনি এখান থেকে আমাদের অনুশীলন ওয়ার্কবুক বিনামূল্যে ডাউনলোড করতে পারেন!

লিনিয়ার প্রোগ্রামিং কি?

লিনিয়ার প্রোগ্রামিং হল একটি গাণিতিক টুল যা বিভিন্ন গাণিতিক ফাংশন এবং সীমাবদ্ধতার মাধ্যমে একটি পরিস্থিতি বিশ্লেষণ করে এবং আপনার উদ্দেশ্যের সর্বোত্তম পয়েন্ট খুঁজে পায়। এই কৌশলটি ব্যবসায়িক বিনিয়োগ, উৎপাদন চক্র, আমাদের প্রয়োজনীয় পণ্য কেনার ক্ষেত্রে, ইত্যাদি অপ্টিমাইজ করতে ব্যাপকভাবে ব্যবহৃত হয়৷

লিনিয়ার প্রোগ্রামিং এর মৌলিক উপাদানগুলি

• ডিসিশন ভেরিয়েবল: রৈখিক প্রোগ্রামিংয়ের মাধ্যমে আমাদের উদ্দেশ্যের সর্বোত্তম পয়েন্ট গণনা করার জন্য এই ভেরিয়েবলগুলি প্রয়োজন। আমাদের সিদ্ধান্তের পরিস্থিতি, সীমাবদ্ধতা এবং উদ্দেশ্য ফাংশন এই ভেরিয়েবলগুলির সাথে সেট করা হয়।
• সীমাবদ্ধতা: সীমাবদ্ধতা হল এমন শর্ত যা উদ্দেশ্যমূলক কাজকে সীমাবদ্ধ করে এবং সম্ভাব্য অঞ্চল নির্ধারণ করে। তারা সমতা বা অসমতা উভয়ই হতে পারে।
• অবজেক্টিভ ফাংশন: এটি আপনার উদ্দেশ্য ফাংশন. সর্বোত্তম সমাধান খুঁজে পেতে আপনাকে সঠিক সীমাবদ্ধতার সাথে এই সমীকরণটি সন্তুষ্ট করতে হবে।
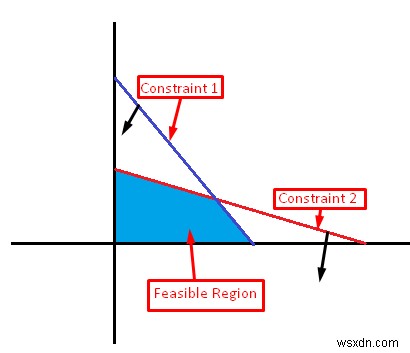
• সম্ভাব্য অঞ্চল: এই অঞ্চলটি যথাযথ সীমাবদ্ধতা প্রয়োগ করার পরে উদ্দেশ্য ফাংশনের সর্বোত্তম অঞ্চল। সর্বোত্তম সমাধান এই অঞ্চলের কোথাও নিহিত।
• সম্ভাব্য সমাধান: সম্ভাব্য সমাধান হল সম্ভাব্য অঞ্চলের কোণার পয়েন্টগুলির জন্য উদ্দেশ্যমূলক ফাংশনের সমাধান৷
• অনুকূল সমাধান: সর্বোত্তম সমাধান হল আপনার উদ্দেশ্য ফাংশনের সর্বোত্তম বিন্দু। আপনি গণনা করা সম্ভাব্য সমাধান থেকে এটি খুঁজে পেতে পারেন।

এক্সেলে রৈখিক প্রোগ্রামিং গ্রাফ করার ধাপগুলি

ধরা যাক, আপনাকে F =6X+8Y হিসাবে একটি উদ্দেশ্যমূলক ফাংশন দেওয়া হয়েছে . আপনাকে সীমাবদ্ধতার সাথে এই ফাংশনটি সর্বাধিক করতে হবে:

2X+4Y <=60

4X+2Y <=48

এখন, নিচের ধাপগুলি ব্যবহার করে আপনি Excel-এ লিনিয়ার প্রোগ্রামিং গ্রাফ করার মাধ্যমে সর্বোত্তম পয়েন্ট খুঁজে পেতে পারেন৷

📌 ধাপ 1:উদ্দেশ্যমূলক ফাংশন এবং সীমাবদ্ধতা লাইন পয়েন্টগুলি রেকর্ড করুন

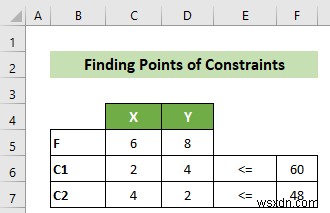
এক্সেলে রৈখিক প্রোগ্রামিং গ্রাফ করার জন্য, প্রথমে এবং সর্বাগ্রে, আপনাকে আপনার উদ্দেশ্য ফাংশন এবং সীমাবদ্ধতার পয়েন্টগুলি রেকর্ড করতে হবে৷

• এটি করার জন্য, প্রথমে উদ্দেশ্য ফাংশন এবং সীমাবদ্ধতার সহগ এবং চিহ্নগুলি সঠিকভাবে রেকর্ড করুন৷

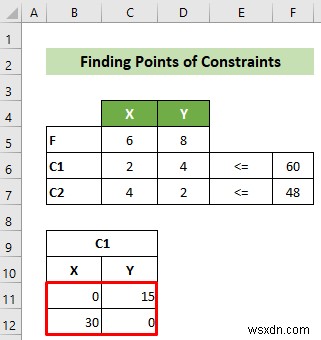
• এখন, প্রথম সীমাবদ্ধতার জন্য, C1, সীমাবদ্ধতা আঁকতে সমীকরণের দুটি বিন্দু খুঁজুন। আপনি X=0 নিয়ে এটি করতে পারেন যা আপনাকে Y 15 হিসাবে দেবে। একইভাবে, Y=0 নিলে X হবে 30।

• পরবর্তীতে, একইভাবে, দ্বিতীয় সীমাবদ্ধতার জন্য দুটি পয়েন্ট খুঁজুন, C2। এখানে, আপনি যদি X=0 নেন, তাহলে আপনি Y কে 24 হিসেবে পাবেন। এবং একইভাবে, Y=0 নিলে আপনি X=12 পাবেন।

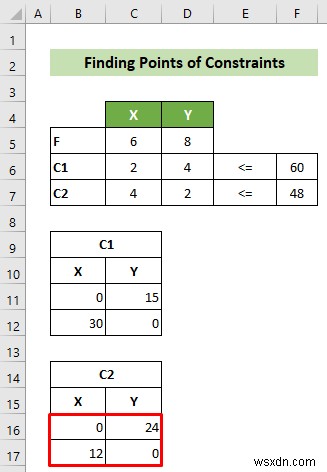
ফলস্বরূপ, আপনার কাছে আপনার উদ্দেশ্য ফাংশন, সীমাবদ্ধতা এবং সীমাবদ্ধতাগুলি আঁকার জন্য দুটি পয়েন্ট সহ একটি ওয়ার্কশীট থাকবে। কার্যপত্রকটি অবশেষে এইরকম দেখাবে৷

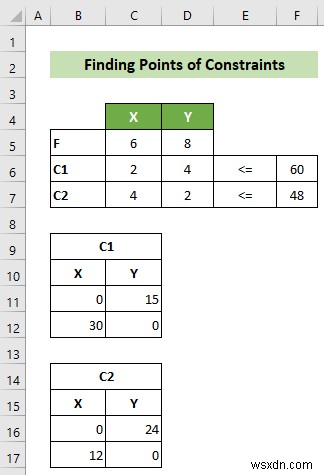
📌 ধাপ 2:সম্ভাব্য অঞ্চল খুঁজুন

প্রথম ধাপ অনুসরণ করে, আপনাকে এখন সম্ভাব্য অঞ্চল খুঁজে বের করতে হবে।

• এটি করার জন্য, প্রাথমিকভাবে, B6:C8 সেল নির্বাচন করুন। পরবর্তীকালে, ঢোকান-এ যান ট্যাব>> চার্ট গ্রুপ>> স্ক্যাটার বা বাবল চার্ট ঢোকান টুল>> মসৃণ লাইনের সাথে ছড়িয়ে দিন বিকল্প।

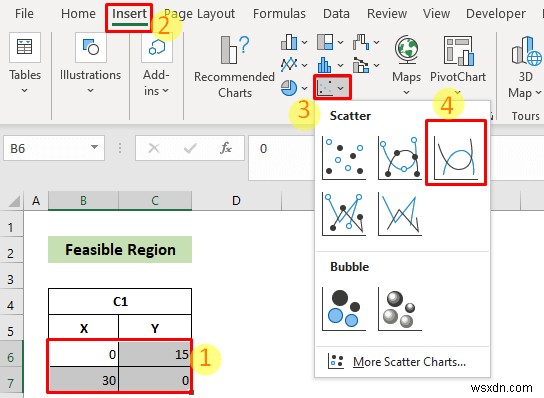
• ফলে, আপনার B6:C8 এর মান অনুযায়ী মসৃণ রেখা সহ একটি স্ক্যাটার প্লট থাকবে। সেল।

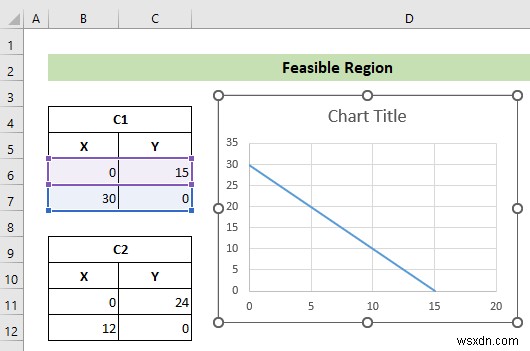
• কিন্তু, প্লটটি আপনার প্রয়োজনীয় বিন্যাসে নেই। তাই, ডান-ক্লিক করুন চার্টে পরবর্তীকালে, ডেটা নির্বাচন করুন... নির্বাচন করুন প্রসঙ্গ মেনু থেকে বিকল্প।

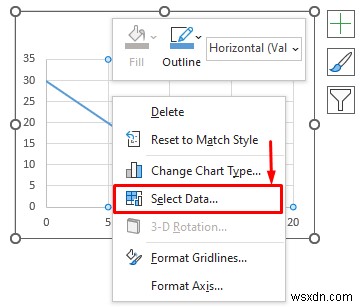
• ফলে, ডেটা উৎস নির্বাচন করুন উইন্ডো প্রদর্শিত হবে। অনুসরণ করে, সিরিজ1 বেছে নিন এখানে বিকল্প এবং সম্পাদনা এ ক্লিক করুন বোতাম।

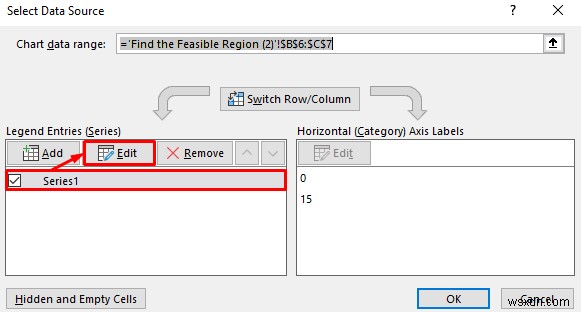
• এই সময়ে, সিরিজ সম্পাদনা করুন উইন্ডো প্রদর্শিত হবে। সিরিজের নামে: টেক্সট বক্স, C1 লিখুন . সিরিজ X মানগুলিতে: পাঠ্য বাক্স, B6:B7 হিসাবে পরিসর নির্বাচন করুন৷ কোষ একইভাবে, সিরিজ Y মানগুলিতে: টেক্সট বক্স, C6:C7 হিসাবে পরিসর নির্বাচন করুন মান শেষ কিন্তু অন্তত নয়, ঠিক আছে এ ক্লিক করুন বোতাম।

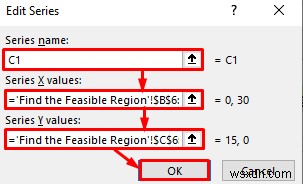
• এখন, আপনি ডেটা উৎস নির্বাচন করুন এ ফিরে আসবেন জানলা. এখানে, যোগ করুন-এ ক্লিক করুন বোতাম।

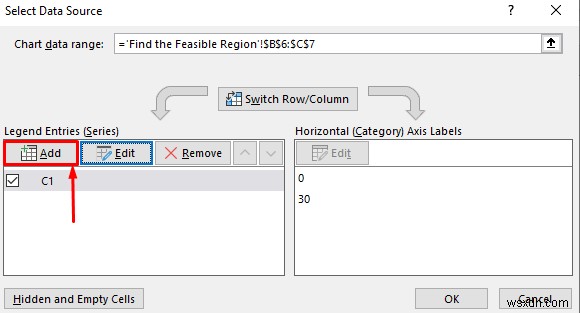
• ফলে, আরেকটি সম্পাদনা সিরিজ উইন্ডো প্রদর্শিত হবে। সিরিজের নামে: টেক্সট বক্স, C2 লিখুন . অনুসরণ করে, সিরিজ X মান: টেক্সট বক্স, B11:B12 হিসাবে ডেটা পরিসর নির্বাচন করুন কোষ একইভাবে, সিরিজ Y মানগুলিতে: টেক্সট বক্স, C11:C12 হিসাবে ডেটা পরিসর নির্বাচন করুন কোষ পরবর্তীকালে, ঠিক আছে এ ক্লিক করুন৷ বোতাম।

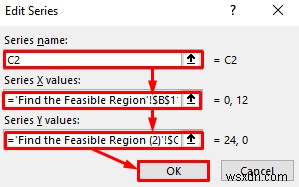
• এখন, আপনি আবার ডেটা উৎস নির্বাচন করুন এ ফিরে আসবেন জানলা. এরপর, ঠিক আছে -এ ক্লিক করুন এখানে বোতাম।

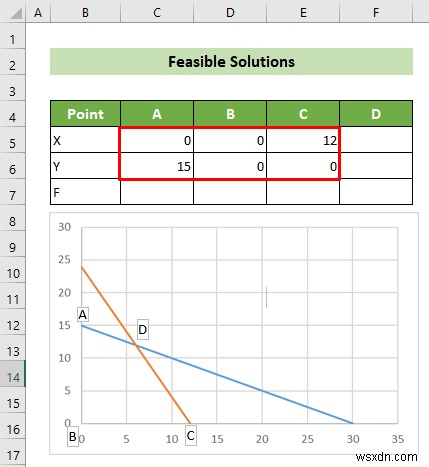
• ফলে, আপনি দেখতে পাবেন আপনার রৈখিক প্রোগ্রামিংয়ের সমস্ত সীমাবদ্ধতার সাথে আপনার একটি স্ক্যাটার গ্রাফ থাকবে। এবং, গ্রাফটি এইরকম হওয়া উচিত।

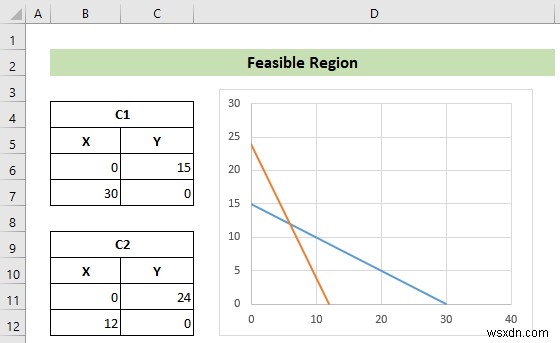
• এখন, যেহেতু উভয় সীমাবদ্ধতাই কম বা সমান অসমতার মধ্যে রয়েছে, উভয় সীমাবদ্ধ রেখাই উৎপত্তির দিকে পরিচালিত হবে। ফলস্বরূপ, সম্ভাব্য এলাকাটি নিম্নলিখিত চিত্রের মত হবে।

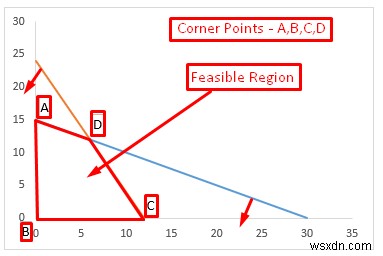
সুতরাং, ABCD হল সম্ভাব্য অঞ্চল, এবং A, B, C, এবং D হল এই অঞ্চলের কোণ বিন্দু।

📌 ধাপ 3:সর্বোত্তম সমাধান খুঁজুন

সম্ভাব্য অঞ্চল নির্ধারণ করার পরে, আপনাকে এখনই সম্ভাব্য সমাধানগুলি খুঁজে বের করতে হবে৷

• এটি করার জন্য, একেবারে শুরুতে, আপনাকে কোণার বিন্দুগুলির X এবং Y স্থানাঙ্কগুলি খুঁজে বের করতে হবে। গ্রাফ এবং সীমাবদ্ধতার মান সারণী থেকে, আমরা খুব সহজেই A, B এবং C পয়েন্টগুলি খুঁজে পেতে পারি যা যথাক্রমে (0,15), (0,0), এবং (12,0)।

• এখন, বিন্দু D-এর স্থানাঙ্ক খোঁজার জন্য, ঘরগুলি নির্বাচন করুন D5:D6 এবং নিচের সূত্রটি সন্নিবেশ করুন যাতে MMULT জড়িত এবং MINVERSE ফাংশন এরপরে, Ctrl+Shift+Enter টিপুন .

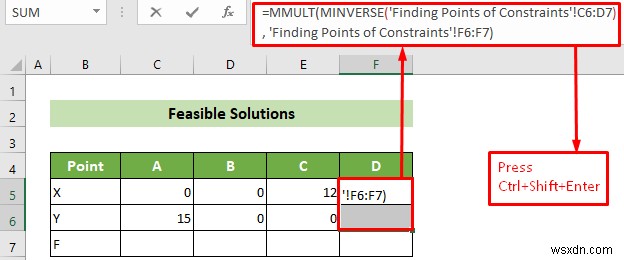
🔎 সূত্র ব্রেকডাউন:

• MINVERSE('Finding Points of Constraints'!C6:D7)

এটি বিপরীত প্রদান করে সীমাবদ্ধতার ওয়ার্কশীটের C6:D7 ফাইন্ডিং পয়েন্টের ম্যাট্রিক্স কোষের মান।

ফলাফল :(-0.166666667, 0.333333333) এবং (0.333333333, -0.166666667)

• =MMULT(MINVERSE('Finding Points of Constraints'!C6:D7), 'Finding Points of Constraints'!F6:F7)

এটি ম্যাট্রিক্স পণ্য প্রদান করে পূর্ববর্তী ফলাফলের অ্যারে এবং ফাইন্ডিং পয়েন্টস অফ কনস্ট্রেন্টস ওয়ার্কশীটের F6:F7 অ্যারে।

ফলাফল: {6,12}

• ফলে, আপনি দুটি সীমাবদ্ধ রেখার ছেদকারী বিন্দু D এর স্থানাঙ্ক পাবেন।

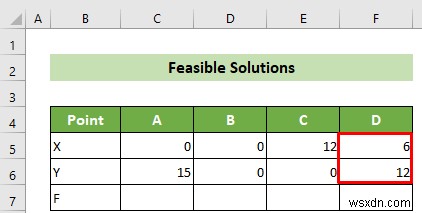
• এখন, আপনার কাছে সমস্ত কর্নার পয়েন্ট আছে। এই সময়ে, আপনাকে এই পয়েন্টগুলি থেকে সম্ভাব্য সমাধান খুঁজে বের করতে হবে। এর জন্য, C7-এ নিচের সূত্রটি লিখুন কোষ পরবর্তীকালে, এন্টার টিপুন বোতাম।

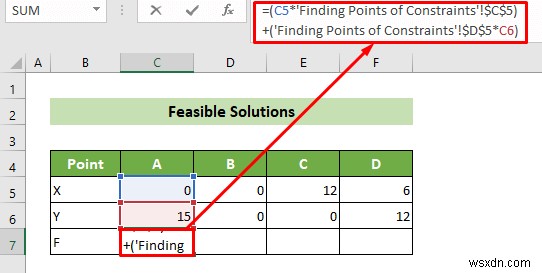
• =(C5*'Finding Points of Constraints'!$C$5)

এটি C5-এর গুণন গণনা করবে সেল মান এবং সীমাবদ্ধতার ওয়ার্কশীটের C5 ফাইন্ডিং পয়েন্টস সেল মান।

ফলাফল: 0

• ('Finding Points of Constraints'!$D$5*C6)

এটি সীমাবদ্ধতার ওয়ার্কশীটের D5 ফাইন্ডিং পয়েন্টগুলিকে গুণ করবে C6 এর সাথে সেল মান বর্তমান ওয়ার্কশীটের কক্ষের মান।

ফলাফল: 120

• =(C5*'Finding Points of Constraints'!$C$5)+('Finding Points of Constraints'!$D$5*C6)

এটি পূর্ববর্তী দুটি ফলাফলের সমষ্টি হবে৷

ফলাফল: 120

• ফলে, আপনি কোণার পয়েন্টের জন্য আপনার উদ্দেশ্য ফাংশনের মান পাবেন, A। অনুসরণ করে, আপনার কার্সারটি নীচে ডানদিকে রাখুন। আপনার কোষের অবস্থান। ফলস্বরূপ, ফিল হ্যান্ডেল প্রদর্শিত হবে. এটিকে ডানদিকে টেনে আনুন অন্য সব পয়েন্টের জন্য একই সূত্র কপি করতে।

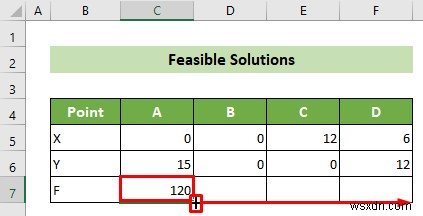
• ফলে, আপনি সমস্ত সম্ভাব্য সমাধান পাবেন৷
৷

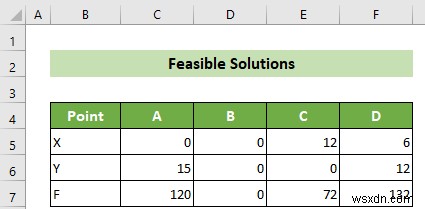
• শেষে কিন্তু অন্তত নয়, গ্রাফের মাধ্যমে আপনার লিনিয়ার প্রোগ্রামিং সমাধান করার জন্য আপনাকে F-এর সর্বোচ্চ মান খুঁজে বের করতে হবে কারণ F-কে সর্বাধিক করার জন্য আপনাকে প্রয়োজন। এখন, আপনি দেখতে পাচ্ছেন যে F-এর সর্বোচ্চ মান হল 132 D (6,12) এ বিন্দু সুতরাং, আপনার সর্বোত্তম পয়েন্ট হল D (6,12) পয়েন্ট।

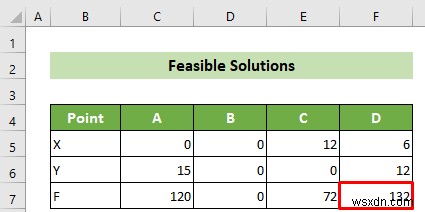
এইভাবে, গ্রাফের মাধ্যমে আপনার লিনিয়ার প্রোগ্রামিং শেষ হয় এবং চূড়ান্ত ফলাফল আসে।

উপসংহার

উপসংহারে, এই নিবন্ধে, আমি আপনাকে এক্সেলে গ্রাফ লিনিয়ার প্রোগ্রামিং করার সমস্ত ধাপ বিস্তারিতভাবে দেখিয়েছি। আমি আপনাকে সম্পূর্ণ নিবন্ধটি সাবধানে পড়ার পরামর্শ দেব এবং আমাদের অনুশীলন ওয়ার্কবুকের সাথে পুঙ্খানুপুঙ্খভাবে অনুশীলন করুন। আমি আশা করি আপনি এই নিবন্ধটি সহায়ক এবং তথ্যপূর্ণ বলে মনে করেন। আপনার যদি আরও কোন প্রশ্ন বা সুপারিশ থাকে, অনুগ্রহ করে নির্দ্বিধায় এখানে মন্তব্য করুন।
এবং, ExcelDemy দেখুন এই মত আরো অনেক নিবন্ধের জন্য. ধন্যবাদ!