একটি আয়তক্ষেত্রে খোদিত একটি বৃত্তের ক্ষেত্রফল যা সি তে একটি অর্ধবৃত্তে খোদাই করা আছে?

একটি আয়তক্ষেত্রে খোদিত একটি বৃত্ত আয়তক্ষেত্রের বৃহত্তর দিকটিকে তার প্রান্ত দিয়ে স্পর্শ করে অর্থাৎ দৈর্ঘ্যটি বৃত্তের স্পর্শক।

একটি অর্ধবৃত্তে খোদাই করা একটি আয়তক্ষেত্র দুটি বিন্দুতে তার চাপকে স্পর্শ করে। আয়তক্ষেত্রের প্রস্থ বৃত্তের ব্যাসের সমান।

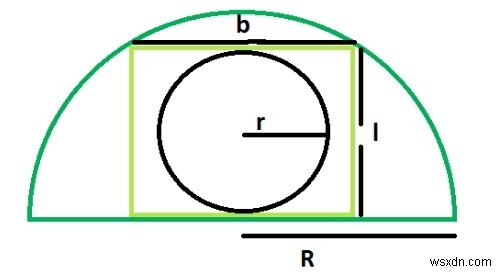
যদি R অর্ধবৃত্তের ব্যাসার্ধ।

আয়তক্ষেত্রের দৈর্ঘ্য =√2R /2

আয়তক্ষেত্রের প্রস্থ =R /√2

খোদিত বৃহত্তম বৃত্তের ব্যাসার্ধ হল

আর =b /2 =R /2√2

এই সূত্রটি ব্যবহার করে আমরা একটি আয়তক্ষেত্রে খোদিত এই বৃত্তের ক্ষেত্রফল খুঁজে পেতে পারি যা একটি অর্ধবৃত্তে খোদাই করা আছে,

ক্ষেত্রফল =(π*r ² ) =π*R/8

উদাহরণ

#include <stdio.h>
int main() {
   float a = 5;
   float area = 3.14 * a/ 8;
   printf("The area of the circle inscribed in a rectangle inscribed in a semicircle of radius %f is %f", a , area);
   return 0;
}

আউটপুট

The area of the circle inscribed in a rectangle inscribed in a semicircle of radius 5.00000 is 1.962500