একটি অর্ধবৃত্তে খোদাই করা একটি বর্গক্ষেত্রের মধ্যে সবচেয়ে বড় রেউলক্স ত্রিভুজ?

এখানে আমরা একটি অর্ধবৃত্তে খোদাই করা একটি বর্গক্ষেত্রের মধ্যে খোদিত বৃহত্তম রিউল্যাক্স ত্রিভুজের ক্ষেত্রফল দেখতে পাব। ধরুন অর্ধবৃত্তের ব্যাসার্ধ হল R, বর্গক্ষেত্রের বাহু হল 'a' এবং Reuleax ত্রিভুজের উচ্চতা হল h৷

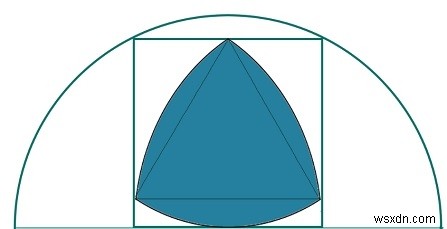
আমরা জানি যে একটি অর্ধবৃত্তে খোদাই করা বর্গক্ষেত্রের দিক হল −

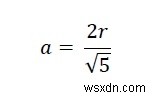
Reuleaux ত্রিভুজের উচ্চতা a এর সমান। তাই a =h. সুতরাং রেউলক্স ত্রিভুজের ক্ষেত্রফল হল −

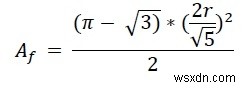
উদাহরণ

#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float r) { //radius of the semicircle is r
   if (r < 0) //if r is negative it is invalid
      return -1;
   float area = ((3.1415 - sqrt(3)) * (2*r/(sqrt(5))) * (2*r/(sqrt(5))))/2;
   return area;
}
int main() {
   float rad = 8;
   cout << "Area of Reuleaux Triangle: " << areaReuleaux(rad);
}

আউটপুট

Area of Reuleaux Triangle: 36.0819