এক্সেলের অনেক বৈশিষ্ট্য রয়েছে যা বিভিন্ন কাজ সম্পাদন করতে পারে। বিভিন্ন পরিসংখ্যানগত এবং আর্থিক বিশ্লেষণ করার পাশাপাশি, আমরা এক্সেলে সমীকরণগুলি সমাধান করতে পারি। এই প্রবন্ধে, আমরা একটি জনপ্রিয় বিষয় বিশ্লেষণ করব যা হল সঠিক চিত্র সহ বিভিন্ন উপায়ে এক্সেলে সমীকরণগুলি সমাধান করা৷
এক্সেল এ সমীকরণ কিভাবে সমাধান করবেন
এক্সেলে সমীকরণগুলি সমাধান করা শুরু করার আগে, আসুন দেখি কোন ধরণের সমীকরণ কোন পদ্ধতিতে সমাধান করা হবে।
এক্সেলে সমাধানযোগ্য সমীকরণের প্রকার:
বিভিন্ন ধরণের সমীকরণ বিদ্যমান। কিন্তু সবগুলোই এক্সেলে সমাধান করা সম্ভব নয়। এই নিবন্ধে, আমরা নিম্নলিখিত ধরণের সমীকরণগুলি সমাধান করব।
- ঘন সমীকরণ,
- চতুর্ঘাতিক সমীকরণ,
- রৈখিক সমীকরণ,
- সূচক সমীকরণ,
- ডিফারেনশিয়াল সমীকরণ,
- নন-লিনিয়ার সমীকরণ
সমীকরণ সমাধানের জন্য এক্সেল টুলস:
এক্সেলের সমীকরণগুলি সমাধান করার জন্য কিছু উত্সর্গীকৃত সরঞ্জাম রয়েছে যেমন এক্সেল সমাধান অ্যাড-ইন এবং লক্ষ্য অন্বেষণ বৈশিষ্ট্য. এছাড়াও, আপনি ম্যাট্রিক্স সিস্টেম ইত্যাদি ব্যবহার করে এক্সেলে সংখ্যাগত/ম্যানুয়ালি সমীকরণগুলি সমাধান করতে পারেন।
Excel এ সমীকরণ সমাধানের ৫টি উদাহরণ
1. এক্সেল
এ বহুপদী সমীকরণ সমাধান করা একটি বহুপদ সমীকরণ হল পাটিগণিত ক্রিয়াকলাপের সাথে ভেরিয়েবল এবং সহগগুলির সংমিশ্রণ।এই বিভাগে, আমরা বিভিন্ন বহুপদী সমীকরণ যেমন ঘন, চতুর্ভুজ, রৈখিক, ইত্যাদি সমাধান করার চেষ্টা করব।
1.1 ঘন সমীকরণ সমাধান করা
একটি বহুপদ ডিগ্রী তিন সহ সমীকরণকে বলা হয় কিউবিক বহুপদী সমীকরণ।এখানে, আমরা এক্সেলে কিউবিক সমীকরণ সমাধানের দুটি উপায় দেখাব।
i. লক্ষ্য অনুসন্ধান ব্যবহার করা
এখানে, আমরা লক্ষ্য অন্বেষণ ব্যবহার করব এই ঘন সমীকরণ সমাধান করার জন্য এক্সেলের বৈশিষ্ট্য।
অনুমান করুন, আমাদের একটি সমীকরণ আছে:
Y=5X 3 -2X 2 +3X-6আমাদের এই সমীকরণটি সমাধান করতে হবে এবং X এর মান বের করতে হবে .
📌 পদক্ষেপ:
- প্রথমে, আমরা সহগকে চারটি কক্ষে বিভক্ত করি।
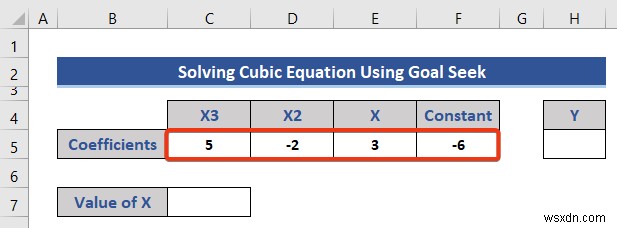
- আমরা X এর মান বের করতে চাই এখানে. X-এর প্রাথমিক মান ধরে নিন হল শূন্য এবং শূন্য (0) সন্নিবেশ করুন সংশ্লিষ্ট কক্ষে।
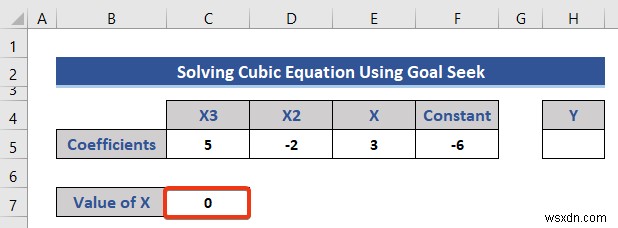
- এখন, Y এর সংশ্লিষ্ট কক্ষের প্রদত্ত সমীকরণটি তৈরি করুন .
- তারপর, এন্টার টিপুন বোতাম এবং Y এর মান পান .
=C5*C7^3+D5*C7^2+E5*C7+F5

- তারপর, এন্টার টিপুন বোতাম এবং Y এর মান পান .
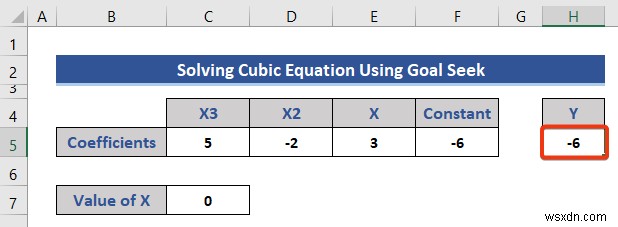
এখন, আমরা লক্ষ্য অন্বেষণ প্রবর্তন করব বৈশিষ্ট্য।
- ডেটা -এ ক্লিক করুন ট্যাব।
- লক্ষ্য অন্বেষণ বেছে নিন কি-ইফ-বিশ্লেষণ থেকে বিকল্প বিভাগ।
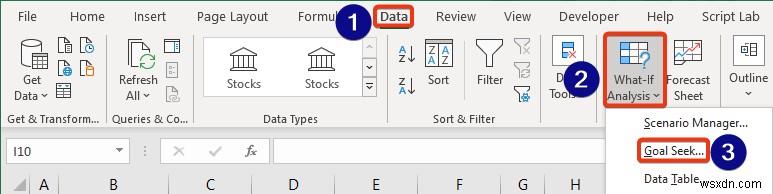
- লক্ষ্য অন্বেষণ ডায়ালগ বক্স প্রদর্শিত হবে।
আমাদের এখানে সেল রেফারেন্স এবং মান সন্নিবেশ করতে হবে।
- সেল H5 বেছে নিন সেট সেল হিসাবে। এই ঘরে সমীকরণ রয়েছে।
- এবং সেল C7 নির্বাচন করুন হিসাবে কক্ষ পরিবর্তন করে , যা পরিবর্তনশীল। এই ভেরিয়েবলের মান অপারেশনের পরে পরিবর্তিত হবে।
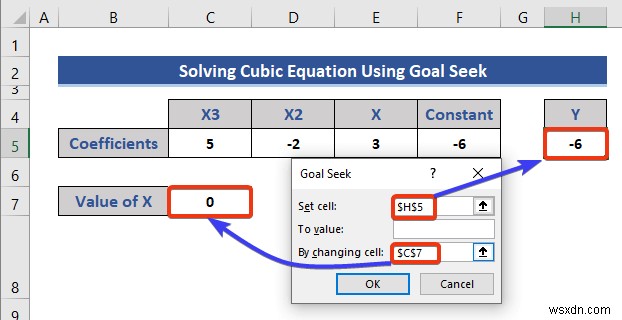
- 20 রাখুন মানে বক্স, যা সমীকরণের জন্য অনুমান করা একটি মান।
- অবশেষে, ঠিক আছে টিপুন বোতাম।
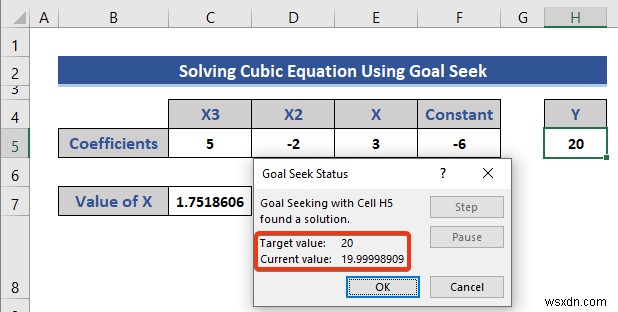
অপারেশনের অবস্থা দেখাচ্ছে। আমাদের প্রদত্ত লক্ষ্য মানের উপর নির্ভর করে, এই অপারেশনটি সেল C7-এ ভেরিয়েবলের মান গণনা করেছে .
- আবার, ঠিক আছে টিপুন সেখানে।
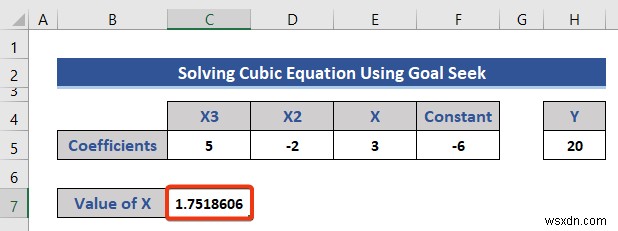
এটি X এর চূড়ান্ত মান .
ii. সলভার অ্যাড-ইন ব্যবহার করা
সমাধানকারী একটি অ্যাড-ইন . এই বিভাগে, আমরা এই সল্ভার ব্যবহার করব প্রদত্ত সমীকরণটি সমাধান করতে এবং ভেরিয়েবলের মান পেতে অ্যাড-ইন করুন।
সমাধানকারী অ্যাড-ইন এক্সেল ডিফল্টে বিদ্যমান নেই। আমাদের প্রথমে এই অ্যাড-ইন যোগ করতে হবে।
📌 পদক্ষেপ:
- আমরা চলকের মান শূন্য (0) সেট করি ডেটাসেটে।
- ফাইল -এ যান>> বিকল্প .
- এক্সেল বিকল্প উইন্ডো প্রদর্শিত হয়৷ ৷
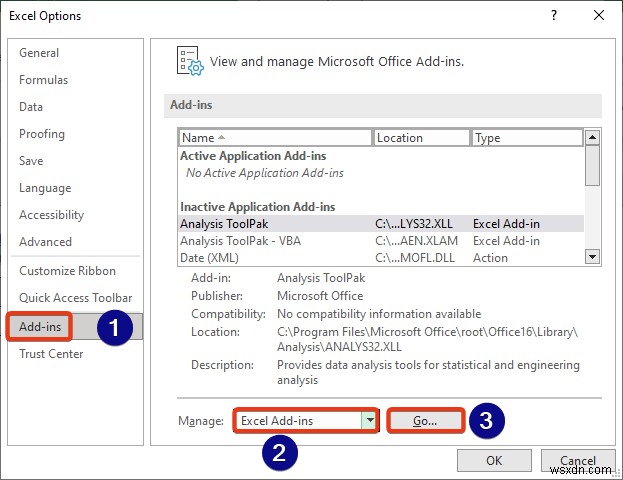
- অ্যাড-ইনস বেছে নিন বাম দিক থেকে।
- এক্সেল অ্যাড-ইনস নির্বাচন করুন এবং যাও -এ ক্লিক করুন বোতাম।
- অ্যাড-ইনস উইন্ডো প্রদর্শিত হয়৷ ৷
- সল্ভার অ্যাড-ইন চেক করুন বিকল্প এবং ঠিক আছে এ ক্লিক করুন .
- আমরা সমাধান দেখতে পাচ্ছি ডেটা -এ অ্যাড-ইন করুন ট্যাব।
- সল্ভার-এ ক্লিক করুন .
- সল্ভার প্যারামিটার উইন্ডো প্রদর্শিত হয়৷ ৷
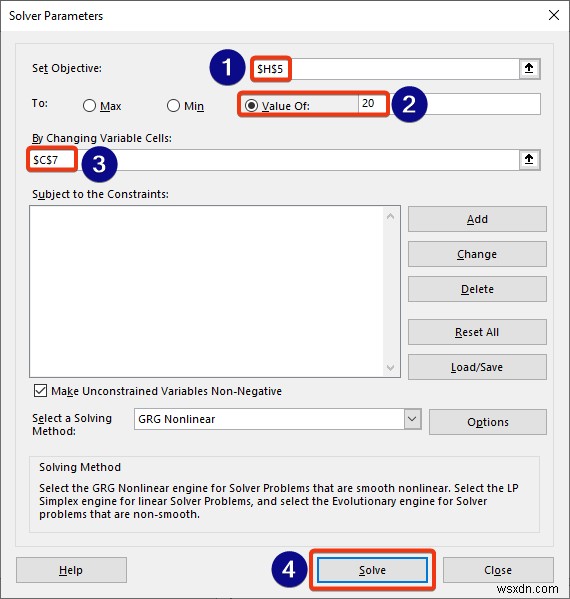
- আমরা সেট অবজেক্ট-এ সমীকরণের সেল রেফারেন্স সন্নিবেশ করি বক্স।
- তারপর, এর মান পরীক্ষা করুন বিকল্প এবং 20 রাখুন সংশ্লিষ্ট বাক্সে।
- ভেরিয়েবল বক্সের সেল রেফারেন্স ঢোকান।
- অবশেষে, সল্ভার-এ ক্লিক করুন .
- Solver সমাধান রাখুন বেছে নিন এবং তারপর ঠিক আছে টিপুন .
- ডেটাসেট দেখুন।
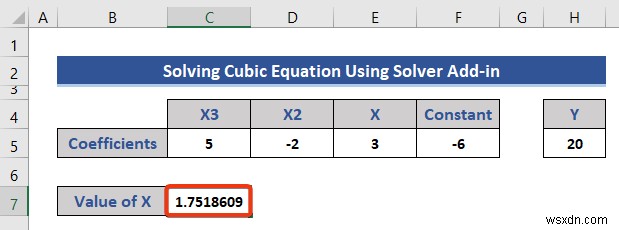
আমরা দেখতে পাচ্ছি ভেরিয়েবলের মান পরিবর্তন করা হয়েছে।
1.2 দ্বিঘাত সমীকরণ সমাধান করা
ডিগ্রী দুই সহ একটি বহুপদী সমীকরণকে চতুর্মুখী বলে বহুপদ সমীকরণএখানে, আমরা এক্সেলে একটি দ্বিঘাত সমীকরণ সমাধান করার দুটি উপায় দেখাব।
আমরা এখানে নিম্নলিখিত দ্বিঘাত সমীকরণটি সমাধান করব।
Y=3X 2 +6X-5i. লক্ষ্য অনুসন্ধান বৈশিষ্ট্য ব্যবহার করে সমাধান করুন
আমরা লক্ষ্য অন্বেষণ ব্যবহার করে এই দ্বিঘাত সমীকরণটি সমাধান করব বৈশিষ্ট্য নীচের বিভাগটি দেখুন৷
৷📌 পদক্ষেপ:
- প্রথমে, আমরা ভেরিয়েবলের সহগ আলাদা করি।
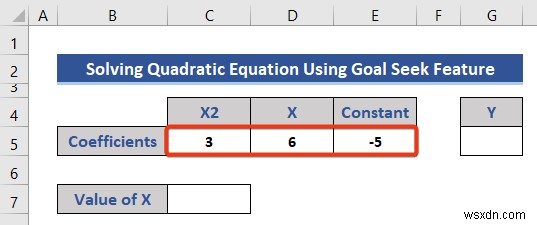
- X এর প্রাথমিক মান সেট করুন শূন্য (0)।
- এছাড়াও, সেল G5-এ সেল রেফারেন্স ব্যবহার করে প্রদত্ত সমীকরণটি সন্নিবেশ করুন .
=C5*C7^2+D5*C7+E5

- এন্টার টিপুন এখন বোতাম।
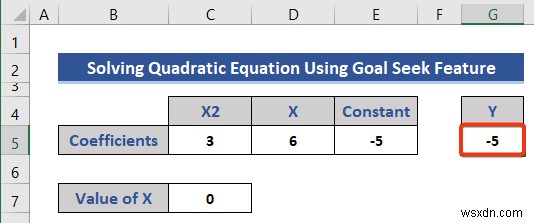
আমরা Y এর মান পাই X বিবেচনা করে শূন্য।
এখন, আমরা লক্ষ্য অন্বেষণ ব্যবহার করব X এর মান পেতে বৈশিষ্ট্য . আমরা ইতিমধ্যে দেখিয়েছি কিভাবে লক্ষ্য অন্বেষণ সক্ষম করতে হয় বৈশিষ্ট্য।
- ভেরিয়েবল এবং সমীকরণের সেল রেফারেন্স লক্ষ্য অন্বেষণ-এ রাখুন ডায়ালগ বক্স
- সমীকরণের মান ধরে নিন 18 এবং এটিকে মানে -এর বাক্সে রাখুন বিভাগ।
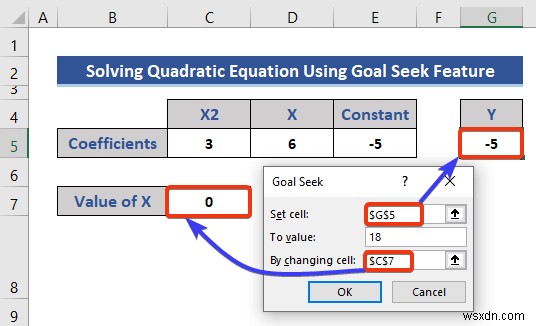
- অবশেষে, ঠিক আছে টিপুন .
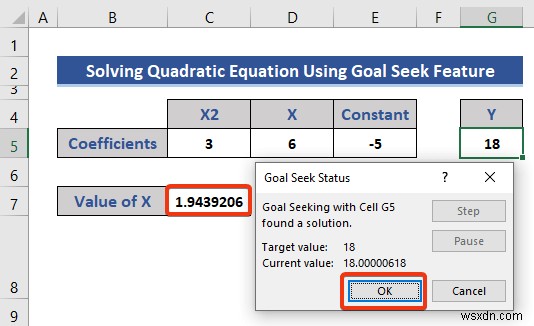
আমরা X ভেরিয়েবলের চূড়ান্ত মান পাই .
ii. সলভার অ্যাড-ইন ব্যবহার করে
আমরা ইতিমধ্যে দেখিয়েছি কিভাবে সল্ভার অ্যাড-ইন যোগ করতে হয় এক্সেলে। এই বিভাগে, আমরা এই সল্ভার ব্যবহার করব নিম্নলিখিত সমীকরণটি সমাধান করতে।
📌 পদক্ষেপ:
- আমরা শূন্য রাখি (0 ) সেল C7 -এ X এর প্রাথমিক মান হিসাবে .
- তারপর, সেল G5-এ নিম্নলিখিত সূত্রটি রাখুন .
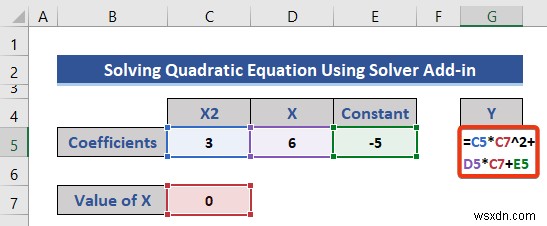
- এন্টার টিপুন বোতাম।
- সল্ভার লিখুন অ্যাড-ইন যেমন আগে দেখানো হয়েছে।
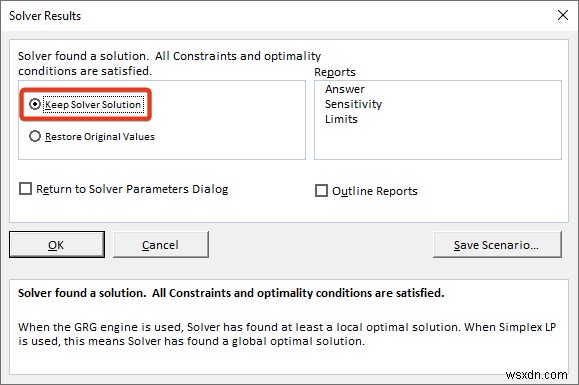
- বস্তু হিসাবে সমীকরণের সেল রেফারেন্স চয়ন করুন।
- ভেরিয়েবলের সেল রেফারেন্স দিন।
- এছাড়া, সমীকরণটির মান 18 হিসাবে সেট করুন .
- অবশেষে, সমাধান এ ক্লিক করুন বিকল্প।
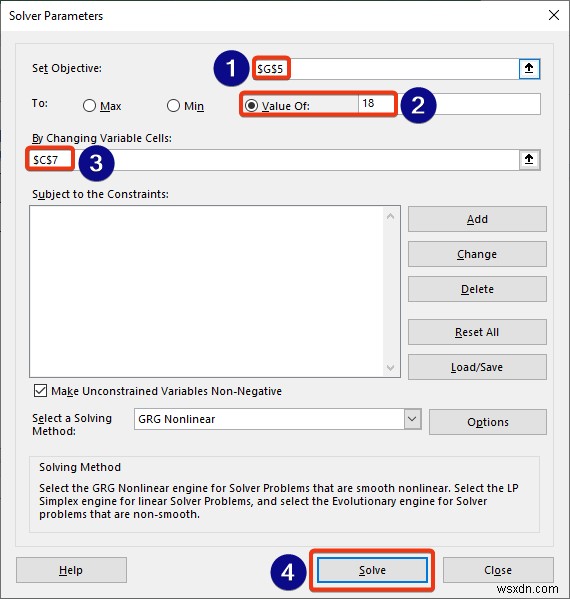
- Keep Solver Solution চেক করুন সমাধান ফলাফল থেকে বিকল্প উইন্ডো।

- অবশেষে, ঠিক আছে ক্লিক করুন বোতাম।
2. রৈখিক সমীকরণ
সমাধান করাএকটি সমীকরণ যাতে 1 এর সর্বোচ্চ ডিগ্রী সহ যেকোনো পরিবর্তনশীল থাকে রৈখিক সমীকরণ বলা হয়।
2.1 ম্যাট্রিক্স সিস্টেম ব্যবহার করা
MINVERSE ফাংশন একটি অ্যারেতে সংরক্ষিত ম্যাট্রিক্সের বিপরীত ম্যাট্রিক্স প্রদান করে।
MMULT ফাংশন দুটি অ্যারের ম্যাট্রিক্স গুণফল প্রদান করে, অ্যারে1 এর মতো একই সংখ্যক সারি সহ একটি অ্যারে এবং অ্যারে2 হিসাবে কলাম .
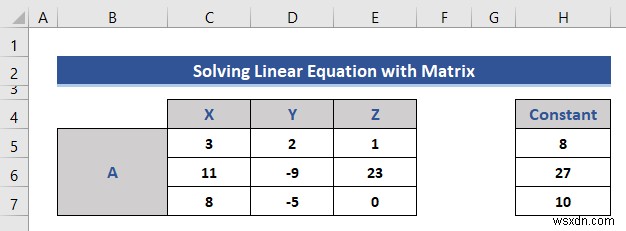
এই পদ্ধতিটি রৈখিক সমীকরণ সমাধান করতে একটি ম্যাট্রিক্স সিস্টেম ব্যবহার করবে। এখানে, 3 রৈখিক সমীকরণ 3 দিয়ে দেওয়া হয় ভেরিয়েবল x , y , এবং z . সমীকরণগুলো হল:
3x+2+y+z=8,
11x-9y+23z=27,
8x-5y=10
আমরা MINVERSE ব্যবহার করব এবং MMULT প্রদত্ত সমীকরণগুলি সমাধান করার জন্য ফাংশন।
📌 পদক্ষেপ:
- প্রথমে, আমরা বিভিন্ন কক্ষে সহগ ভেরিয়েবলকে আলাদা করব এবং তাদের একটি ম্যাট্রিক্স হিসাবে ফর্ম্যাট করব।
- আমরা দুটি ম্যাট্রিক্স করেছি। একটি ভেরিয়েবলের সহগ এবং আরেকটি ধ্রুবক।
- আমরা আমাদের গণনার জন্য আরও দুটি ম্যাট্রিস যোগ করি।
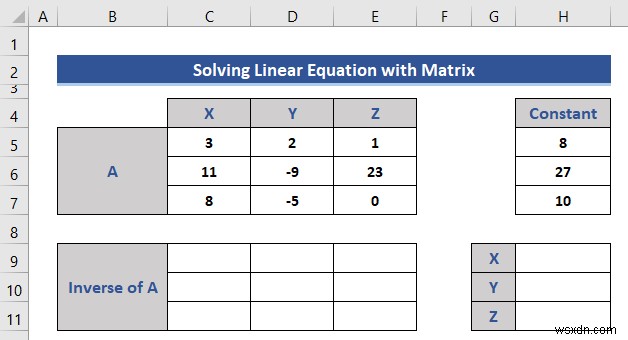
- তারপর, আমরা A এর বিপরীত ম্যাট্রিক্স বের করব MINVERSE ব্যবহার করে ফাংশন।
- নিম্নলিখিত সূত্রটি সেল C7-এ প্রবেশ করান .
=MINVERSE(C5:E7)
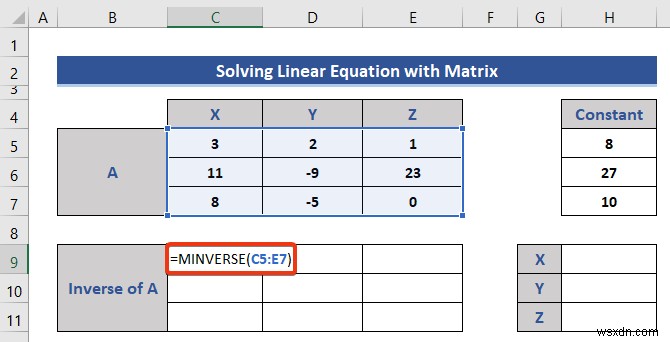
এটি একটি অ্যারে সূত্র৷
৷- এন্টার টিপুন বোতাম।
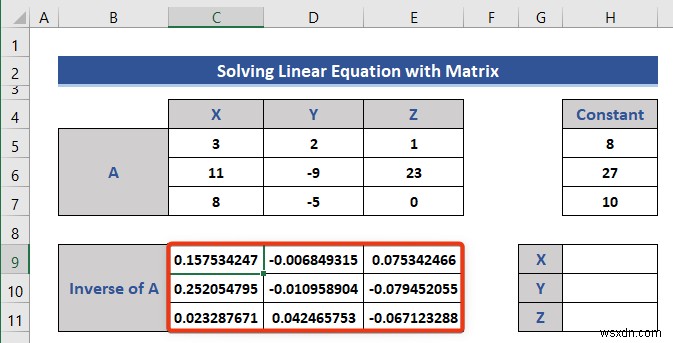
বিপরীত ম্যাট্রিক্স সফলভাবে গঠিত হয়েছে।
- এখন, আমরা MMULT এর উপর ভিত্তি করে একটি সূত্র প্রয়োগ করব সেল H9-এ ফাংশন .
=MMULT(C9:E11,H5:H7)
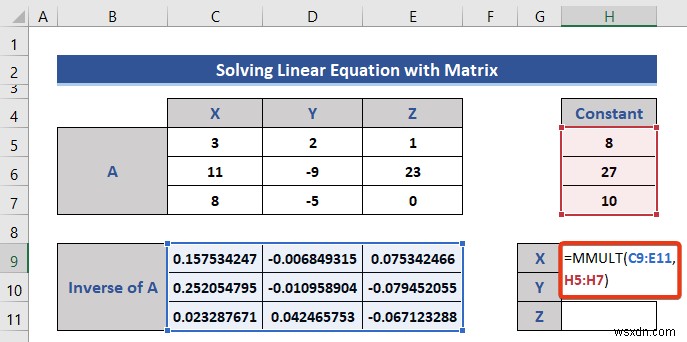
আমরা 3 আকারের দুটি ম্যাট্রিক্স ব্যবহার করেছি x3 এবং 3 x1 সূত্রে এবং ফলস্বরূপ ম্যাট্রিক্সের আকার 3 x1 .
- এন্টার টিপুন আবার বোতাম।
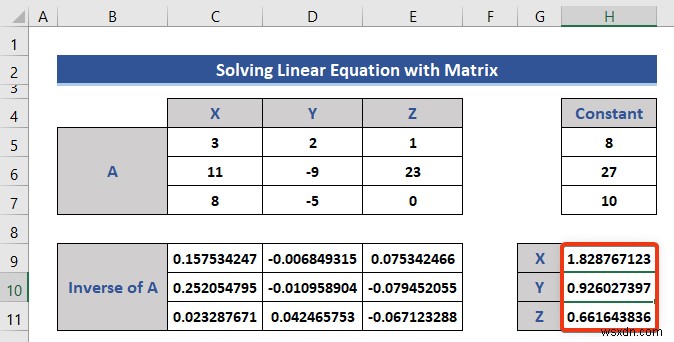
এবং এটি রৈখিক সমীকরণে ব্যবহৃত ভেরিয়েবলের সমাধান।
2.2 সলভার অ্যাড-ইন ব্যবহার করা
আমরা সল্ভার ব্যবহার করব 3 সমাধান করতে অ্যাড-ইন 3 এর সাথে সমীকরণ ভেরিয়েবল।
📌 পদক্ষেপ:
- প্রথমে, আমরা পূর্বে দেখানো সহগগুলিকে আলাদা করি৷
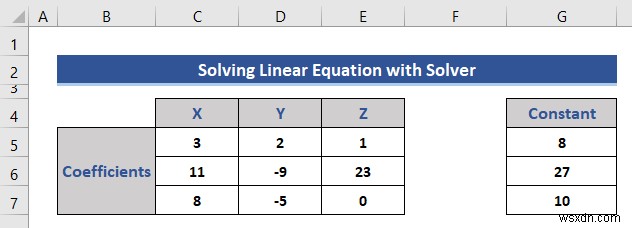
- তারপর, ভেরিয়েবলের মানের জন্য দুটি বিভাগ যোগ করুন এবং সমীকরণ সন্নিবেশ করুন।
- আমরা ভেরিয়েবলের প্রাথমিক মান শূন্য সেট করেছি (0 )।
- সেলে E10 নিচের তিনটি সমীকরণ সন্নিবেশ করান E12 থেকে .
=C5*C10+D5*C11+E5*C12 =C6*C10+D6*C11+E6*C12 =C7*C10+D7*C11+E7*C12
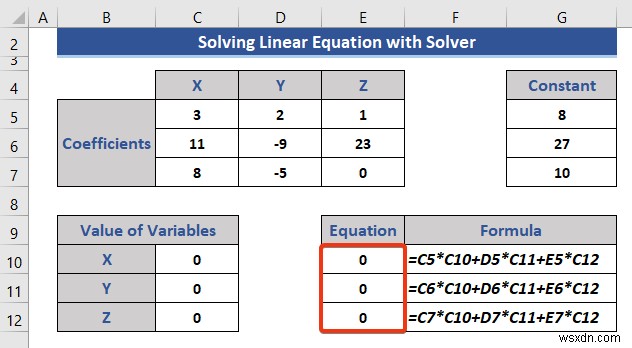
- এখন, সল্ভার-এ যান বৈশিষ্ট্য।
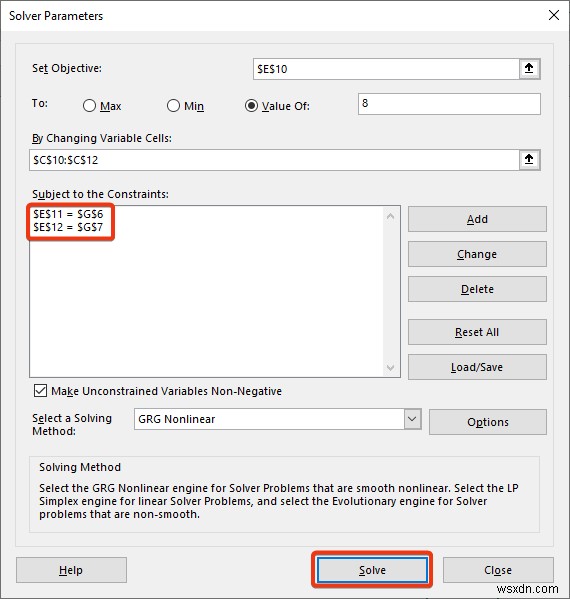
- উদ্দেশ্য হিসেবে ১ম সমীকরণের সেল রেফারেন্স সেট করুন।
- সমীকরণের মান সেট করুন 8 .
- চিহ্নিত বাক্সে ভেরিয়েবলের পরিসীমা সন্নিবেশ করান।
- তারপর, যোগ করুন ক্লিক করুন বোতাম।
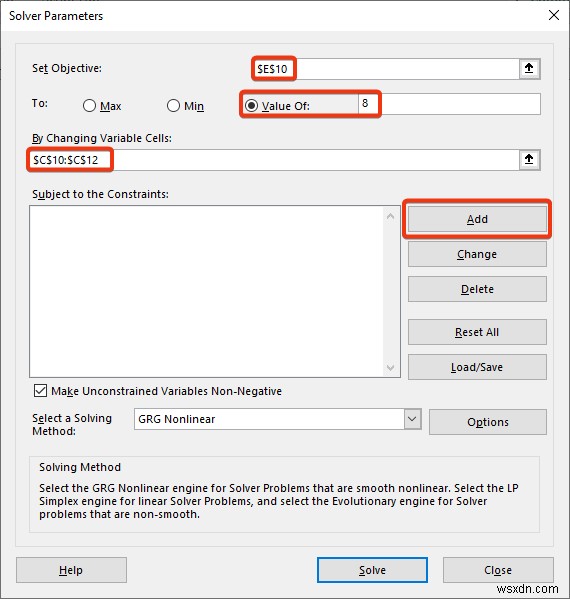
- সংবদ্ধতা যোগ করুন উইন্ডো প্রদর্শিত হয়।
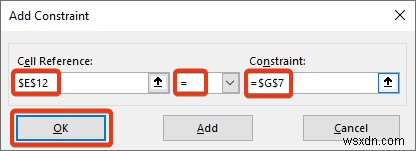
- নিচের ছবিতে চিহ্নিত সেল রেফারেন্স এবং মানগুলি রাখুন৷ ৷
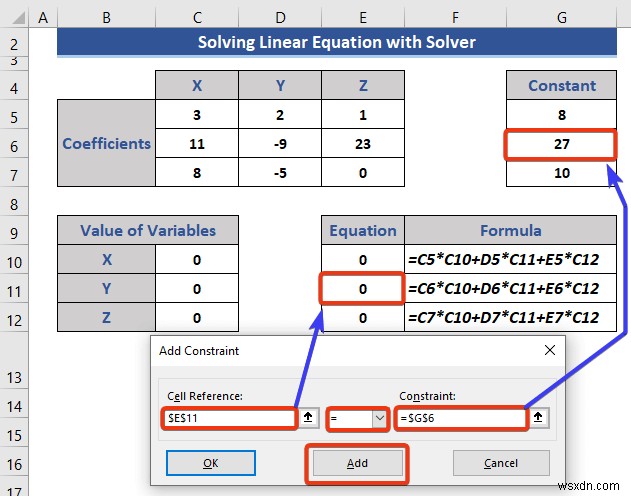
- দ্বিতীয় সীমাবদ্ধতা প্রবেশ করান৷ ৷
- অবশেষে, ঠিক আছে টিপুন .
- সীমাবদ্ধতা যোগ করা হয়েছে। সমাধান টিপুন বোতাম।
- ডেটাসেট দেখুন।
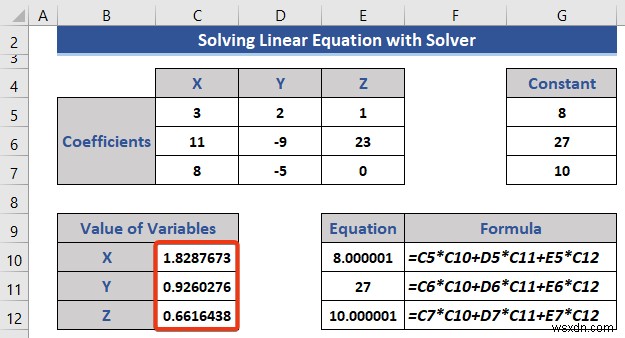
আমরা দেখতে পাচ্ছি ভেরিয়েবলের মান পরিবর্তন করা হয়েছে।
2.3 এক্সেলে 3টি ভেরিয়েবল সহ যুগপত সমীকরণ সমাধানের জন্য ক্র্যামারের নিয়ম ব্যবহার করা
যখন দুই বা ততোধিক রৈখিক সমীকরণের একই চলক থাকে এবং একই সময়ে সমাধান করা যায় তখন তাকে যুগপত সমীকরণ বলে। আমরা Cramer’s ব্যবহার করে যুগপত সমীকরণগুলি সমাধান করব নিয়ম. ফাংশন MDETERM নির্ধারক খুঁজে বের করতে ব্যবহার করা হবে।
MDETERM ফাংশন একটি অ্যারের ম্যাট্রিক্স নির্ধারক প্রদান করে।📌 পদক্ষেপ:
- গুণগুলিকে LHS -এ আলাদা করুন এবং RHS .
- আমরা 4 যোগ করি বিদ্যমান ডেটা ব্যবহার করে একটি ম্যাট্রিক্স তৈরি করার জন্য বিভাগ।

- আমরা LHS এর ডেটা ব্যবহার করব ম্যাট্রিক্স ডি নির্মাণ করতে .
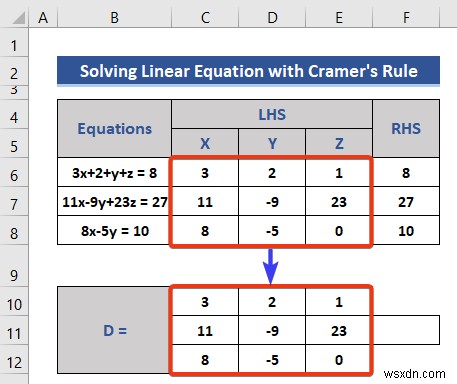
- এখন, আমরা Matrix Dx নির্মাণ করব
- শুধু X এর সহগ প্রতিস্থাপন করুন RHS এর সাথে .
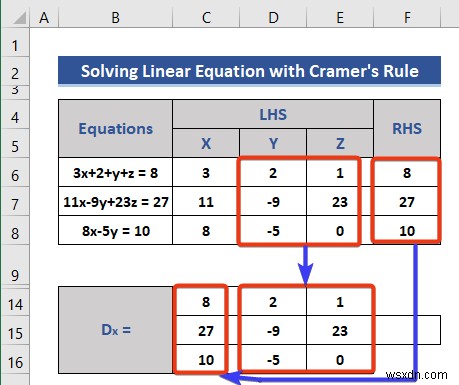
- একইভাবে, Dy গঠন করুন এবং Dz ম্যাট্রিক্স।
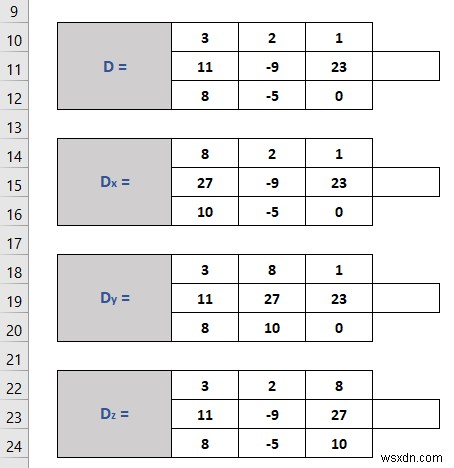
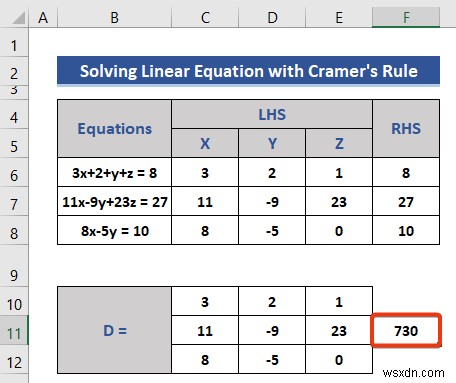
- নিম্নলিখিত সূত্রটি সেল F11 -এ রাখুন Matrix D এর নির্ধারক পেতে .
=MDETERM(C10:E12)
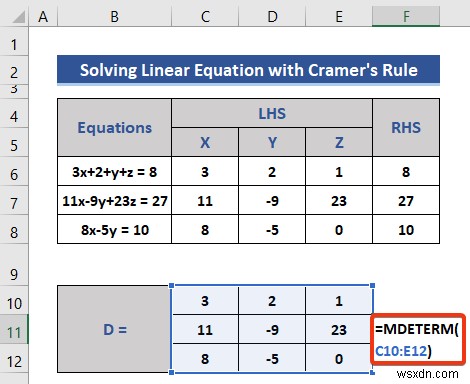
- এন্টার টিপুন বোতাম।
- একইভাবে, নিম্নলিখিত সূত্রগুলি প্রয়োগ করে Dx, Dy এবং Dz-এর নির্ধারকগুলি খুঁজুন৷
=MDETERM(C14:E16 ) =MDETERM(C18:E20) =MDETERM(C22:E24)
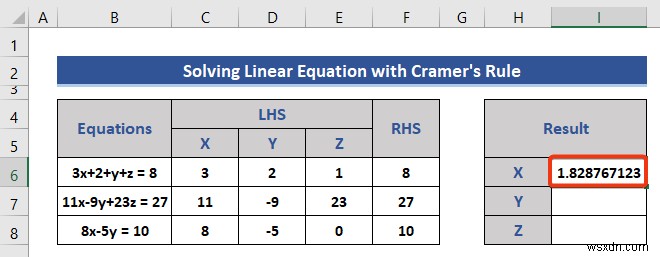
- সেল I6-এ সরান .
- Dx এর নির্ণায়ককে ভাগ করুন D দ্বারা X এর মান গণনা করতে .
=F15/F11
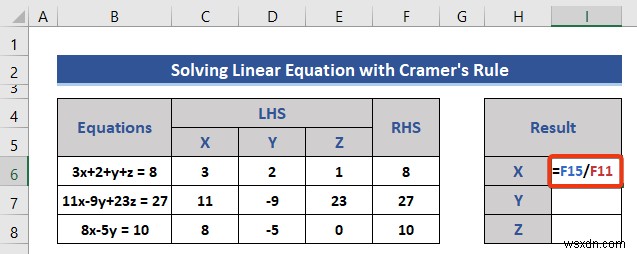
- এন্টার টিপুন ফলাফল পেতে বোতাম।

- একইভাবে, Y এর মান পান এবং Z নিম্নলিখিত সূত্র ব্যবহার করে:
=F19/F11 =F23/F11
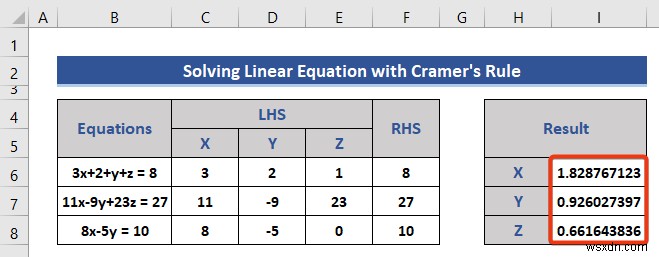
অবশেষে, আমরা যুগপৎ সমীকরণ সমাধান করি এবং তিনটি চলকের মান পাই।
3. এক্সেলে অরৈখিক সমীকরণ সমাধান করা
2 ডিগ্রী সহ একটি সমীকরণ অথবা 2 এর বেশি এবং যেটি সরলরেখা তৈরি করে না তাকে নন-লিনিয়ার সমীকরণ বলেএই পদ্ধতিতে, আমরা সল্ভার ব্যবহার করে এক্সেলের অ-রৈখিক সমীকরণগুলি সমাধান করব এক্সেলের বৈশিষ্ট্য।
আমাদের এখানে দুটি অ-রৈখিক সমীকরণ রয়েছে।
📌 পদক্ষেপ:
- আমরা ডেটাসেটে সমীকরণ এবং ভেরিয়েবল সন্নিবেশ করি।
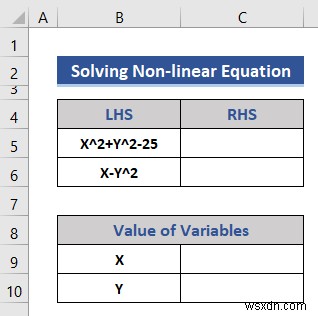
- প্রথম, আমরা শূন্য চলকের মান বিবেচনা করি (0 ) এবং ডেটাসেটে ঢোকান।
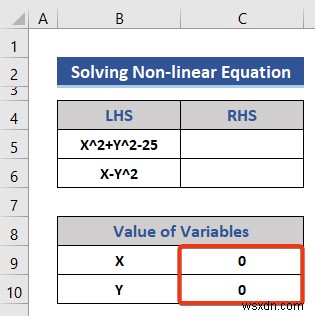
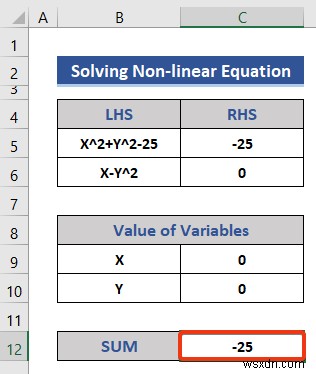
- এখন, সেল C5 -এ দুটি সমীকরণ সন্নিবেশ করান এবং C6 RHS এর মান পেতে .
=C9^2+C10^2-25 =C9-C10^2
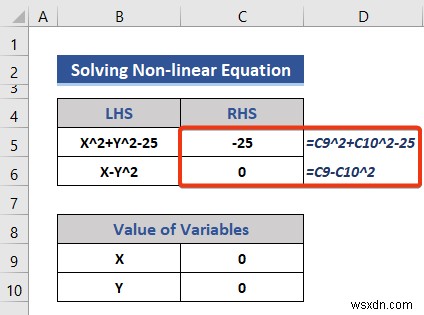
- আমরা যোগফলের জন্য ডেটাসেটে একটি নতুন সারি যোগ করি।
- এর পর, নিচের সমীকরণটি সেল C12-এ রাখুন .
=SUM(C5:C6)
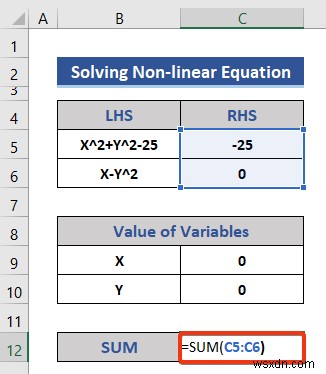
- এন্টার টিপুন বোতাম এবং RHS এর যোগফল উভয় সমীকরণের।
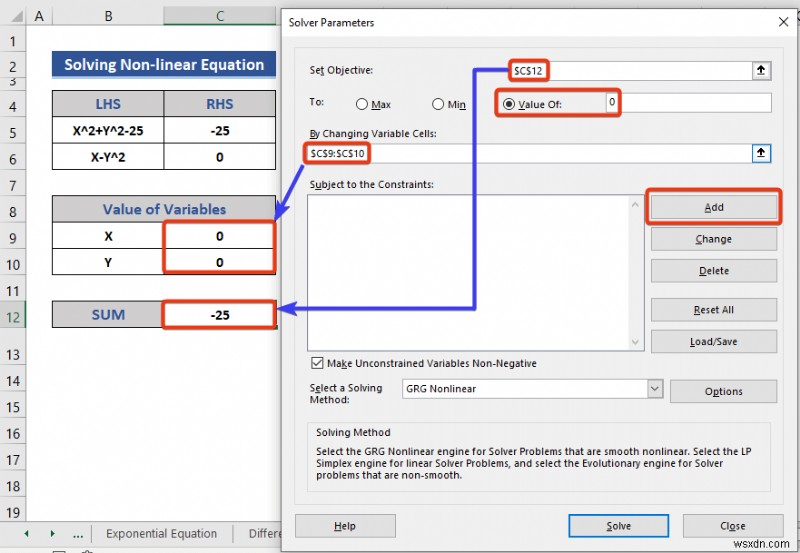
- এখানে, আমরা সল্ভার প্রয়োগ করব এক্সেলের বৈশিষ্ট্য।
- চিহ্নিত বাক্সে ঘরের রেফারেন্স ঢোকান।
- 0-এর মান সেট করুন।
- তারপর, যোগ করুন এ ক্লিক করুন সীমাবদ্ধতা যোগ করার জন্য বোতাম।
- আমরা 1ম যোগ করি ছবিতে দেখানো সীমাবদ্ধতা।
- আবার, যোগ করুন টিপুন 2য় -এর জন্য বোতাম সীমাবদ্ধতা।
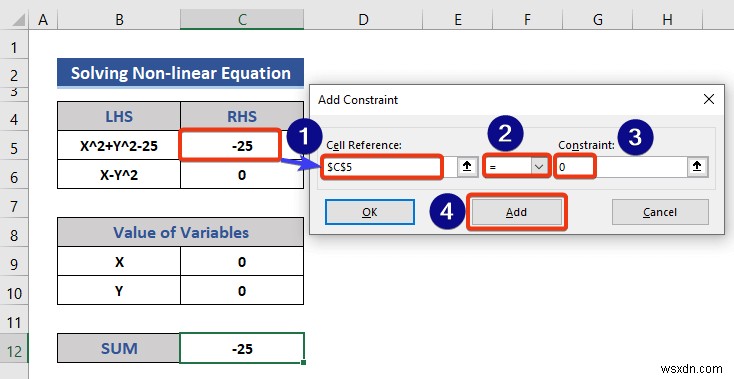
- কোষের রেফারেন্স এবং মান ইনপুট করুন।
- অবশেষে, ঠিক আছে টিপুন .
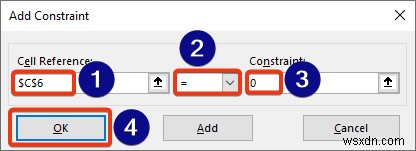
- আমরা দেখতে পাচ্ছি সল্ভারে সীমাবদ্ধতা যোগ করা হয়েছে .
- সল্ভার-এ ক্লিক করুন বোতাম।
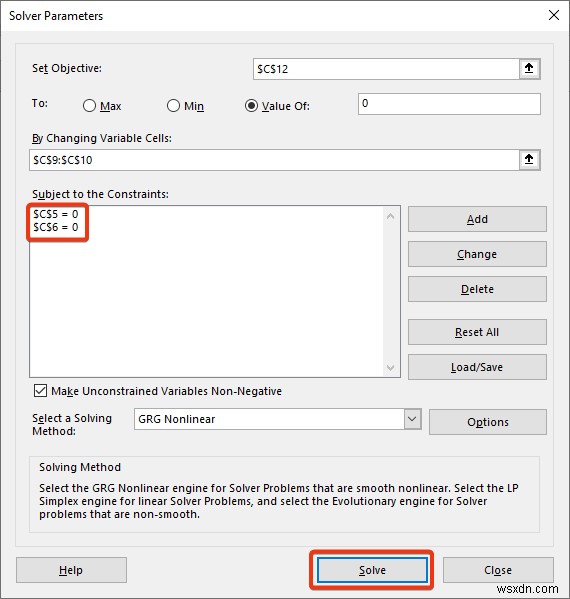
- Keep Solver Solution চেক করুন বিকল্প এবং তারপর ঠিক আছে এ ক্লিক করুন .
- এখন ডেটাসেট দেখুন।
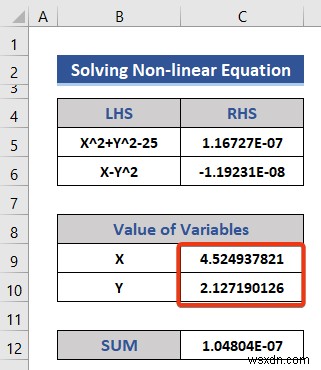
আমরা X এর মান পাই এবং Y সফলভাবে৷
৷4. একটি সূচকীয় সমীকরণ
সমাধান করা সূচক সমীকরণ পরিবর্তনশীল এবং ধ্রুবক সহ। সূচকীয় সমীকরণে, পরিবর্তনশীলটিকে ভিত্তি বা ধ্রুবকের শক্তি বা ডিগ্রি হিসাবে বিবেচনা করা হয়।এই পদ্ধতিতে, আমরা দেখাব কিভাবে EXP ব্যবহার করে একটি সূচকীয় সমীকরণ সমাধান করা যায়। ফাংশন।
EXP ফাংশন ৷ একটি প্রদত্ত সংখ্যার শক্তিতে উত্থাপিত e প্রদান করে।আমরা একটি লক্ষ্য বৃদ্ধির হার সহ একটি এলাকার ভবিষ্যত জনসংখ্যা গণনা করব। আমরা এর জন্য নিচের সমীকরণটি অনুসরণ করব।
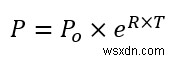
এখানে,
Po =বর্তমান বা প্রাথমিক জনসংখ্যা
আর =বৃদ্ধির হার
টি =সময়
P =ভবিষ্যৎ জনসংখ্যার জন্য সম্মানিত।
এই সমীকরণটির একটি সূচকীয় অংশ রয়েছে, যার জন্য আমরা EXP ব্যবহার করব ফাংশন।
📌 পদক্ষেপ:
- এখানে, বর্তমান জনসংখ্যা, লক্ষ্য বৃদ্ধির হার, এবং বছরের সংখ্যা ডেটাসেটে দেওয়া আছে। আমরা সেই মানগুলি ব্যবহার করে ভবিষ্যতের জনসংখ্যা গণনা করব।
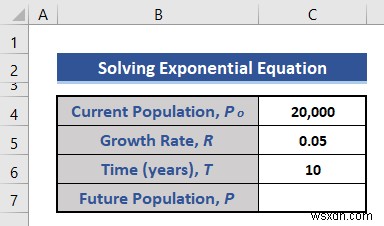
- EXP এর উপর ভিত্তি করে নিম্নলিখিত সূত্রটি রাখুন সেল C7-এ ফাংশন .
=ROUND(C4*EXP(C5*C6),0)
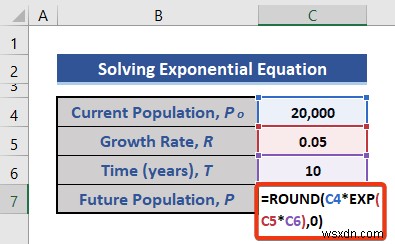
আমরা রাউন্ড ব্যবহার করেছি ফাংশন, যেহেতু জনসংখ্যা অবশ্যই একটি পূর্ণসংখ্যা হতে হবে।
- এখন, এন্টার টিপুন ফলাফল পেতে বোতাম।
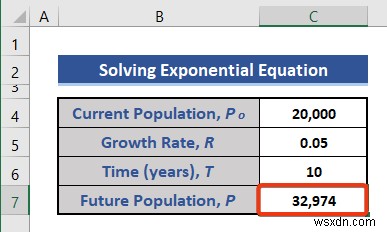
এটি 10 এর পরের ভবিষ্যত জনসংখ্যা অনুমিত বৃদ্ধির হার অনুযায়ী বছর।
5. এক্সেলে ডিফারেনশিয়াল সমীকরণ সমাধান করা
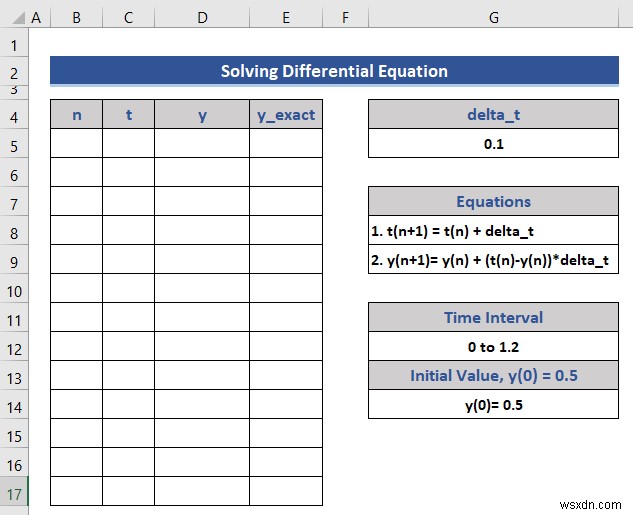
একটি সমীকরণ যাতে একটি অজানা ফাংশনের অন্তত একটি ডেরিভেটিভ থাকে তাকে বলা হয় ডিফারেনশিয়াল সমীকরণ ডেরিভেটিভ সাধারণ বা আংশিক হতে পারে।এখানে, আমরা দেখাব কিভাবে এক্সেলে একটি ডিফারেনশিয়াল সমীকরণ সমাধান করা যায়। আমাদের খুঁজে বের করতে হবে dy/dt , y এর পার্থক্য t সংক্রান্ত . আমরা ডেটাসেটে সমস্ত তথ্য উল্লেখ করেছি৷
৷
📌 পদক্ষেপ:
- প্রাথমিক মান সেট করুন n , t , এবং y প্রদত্ত তথ্য থেকে।

- নিম্নলিখিত সূত্রটি সেল C6-এ রাখুন t এর জন্য .
=C5+$G$5
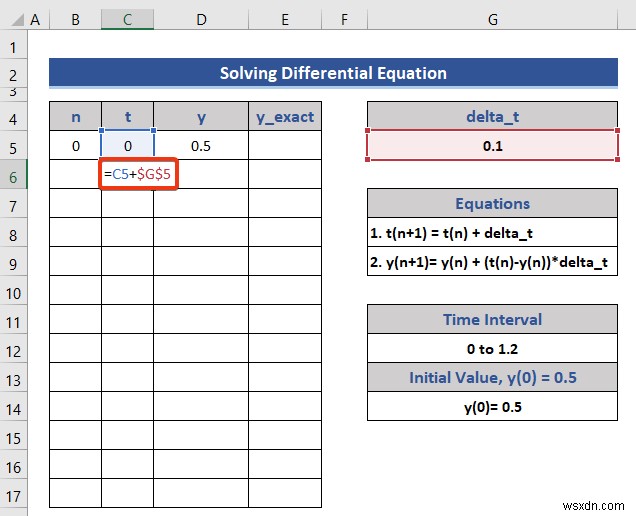
এই সূত্রটি t(n-1) থেকে তৈরি করা হয়েছে .
- এখন, Enter টিপুন বোতাম।
- সেল D6-এ আরেকটি সূত্র রাখুন y এর জন্য .
=D5+(C5-D5)*$G$5
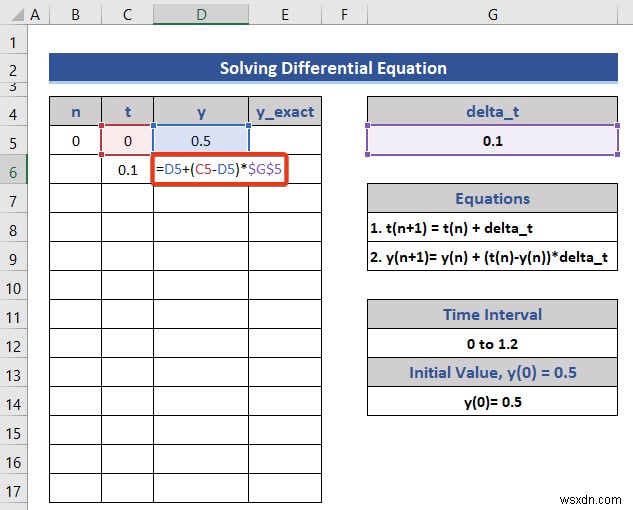
এই সূত্রটি y(n+1) এর সমীকরণ থেকে তৈরি করা হয়েছে .
- আবার, Enter টিপুন বোতাম।
- এখন, মানগুলিকে t-এর সর্বোচ্চ মান পর্যন্ত প্রসারিত করুন , যা হল 1.2 .
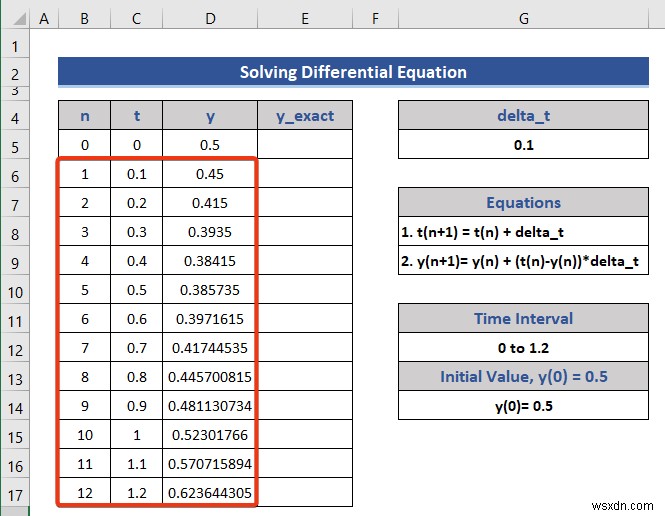
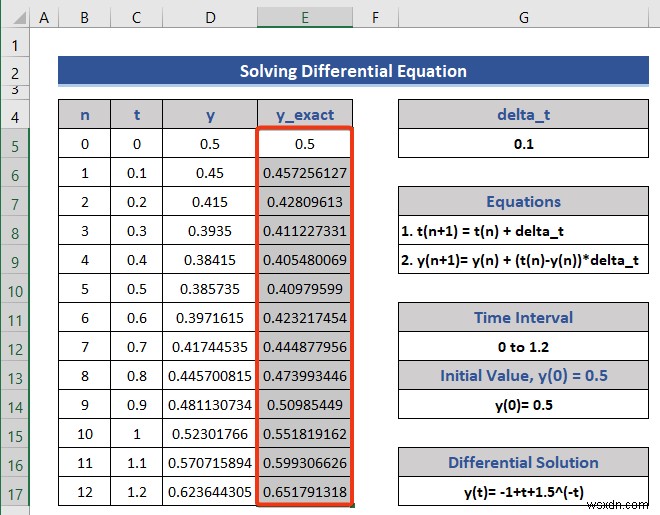
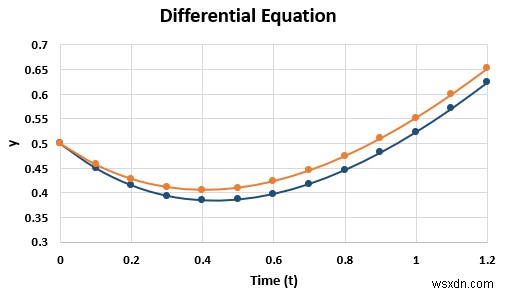
আমরা t এর মান ব্যবহার করে একটি গ্রাফ আঁকতে চাই এবং y .
- সন্নিবেশ এ যান ট্যাব।
- চার্ট থেকে একটি গ্রাফ চয়ন করুন গ্রুপ।
- গ্রাফটি দেখুন।
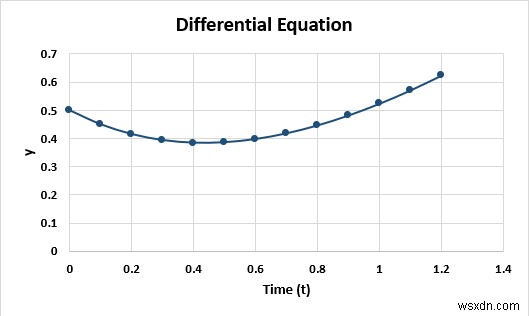
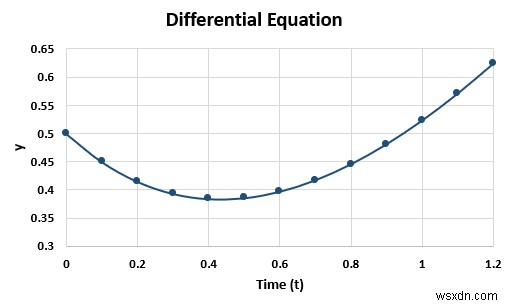
এটি একটি y বনাম t গ্রাফ।
- এখন, গ্রাফে ডাবল ক্লিক করুন এবং গ্রাফ অক্ষের সর্বনিম্ন ও সর্বোচ্চ মান। অনুভূমিক রেখার আকার পরিবর্তন করুন।
- এর পরে, উল্লম্ব লাইনের আকার পরিবর্তন করুন।
- অক্ষ কাস্টমাইজ করার পরে, আমাদের গ্রাফটি এরকম দেখায়।
এখন, আমরা ডিফারেনশিয়াল সমীকরণ খুঁজে বের করব।
- ডিফারেনশিয়াল সমীকরণটি ম্যানুয়ালি গণনা করুন এবং এটিকে ডেটাসেটে রাখুন।
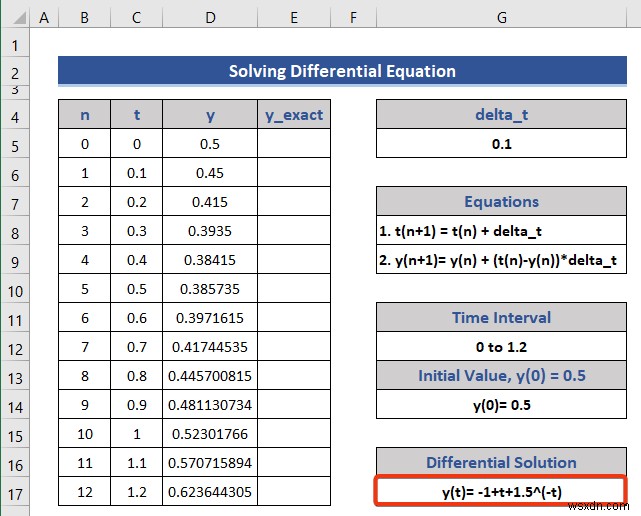
- এর পরে, এই সমীকরণের উপর ভিত্তি করে একটি সমীকরণ তৈরি করুন এবং সেটিকে সেল E5-এ রাখুন .
=-1+C5+1.5*EXP(-C5)
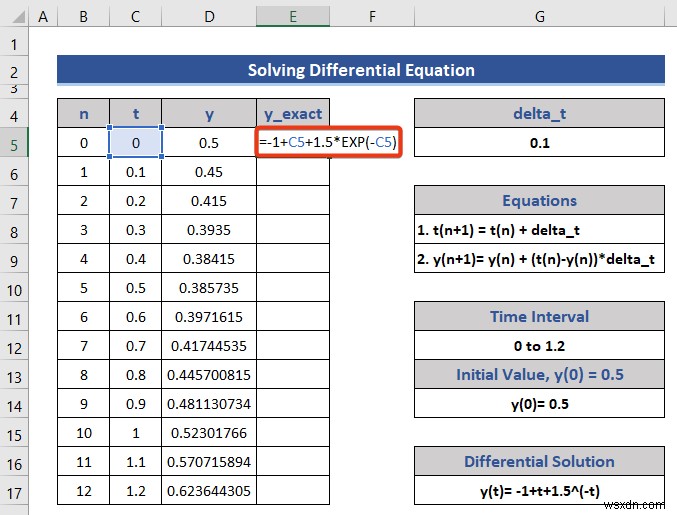
- এন্টার টিপুন বোতাম এবং ফিল হ্যান্ডেল টেনে আনুন আইকন।
- আবার, গ্রাফে যান এবং মাউসের ডান বোতাম টিপুন।
- ডেটা নির্বাচন করুন বেছে নিন প্রসঙ্গ মেনু থেকে বিকল্প .
- যোগ করুন নির্বাচন করুন ডেটা উৎস নির্বাচন করুন থেকে বিকল্প উইন্ডো।
- t এর ঘরগুলি বেছে নিন X -এ কলাম y_exact এর মান এবং কক্ষ Y -এ কলাম সম্পাদনা সিরিজ -এর মান উইন্ডো।
- আবার, গ্রাফটি দেখুন।
উপসংহার
এই নিবন্ধে, আমরা বর্ণনা করেছি কিভাবে বিভিন্ন ধরনের সমীকরণ সমাধান করা যায়। আমি আশা করি এটি এক্সেলের বিভিন্ন সমীকরণ সমাধানে আপনার চাহিদা পূরণ করবে। অনুগ্রহ করে আমাদের ওয়েবসাইট Exceldemy.com দেখুন এবং কমেন্ট বক্সে আপনার পরামর্শ দিন।


