সবচেয়ে বড় রেউলক্স ত্রিভুজটি একটি বর্গক্ষেত্রের মধ্যে খোদাই করা হয়েছে যা C এ একটি উপবৃত্তের মধ্যে খোদাই করা আছে?

একটি রিউলক্স ত্রিভুজ তিনটি বৃত্তাকার ডিস্কের ছেদ থেকে গঠিত একটি আকৃতি, প্রতিটির কেন্দ্র অন্য দুটির সীমানায় থাকে। এর সীমানা হল ধ্রুবক প্রস্থের একটি বক্ররেখা, বৃত্তটি ব্যতীত এই ধরনের বক্ররেখা সবচেয়ে সহজ এবং সর্বাধিক পরিচিত। ধ্রুবক প্রস্থ মানে প্রতিটি দুটি সমান্তরাল সমর্থনকারী রেখার বিচ্ছেদ একই, তাদের অভিযোজন থেকে স্বাধীন। কারণ এর সকল ব্যাস একই।

একটি Reuleaux ত্রিভুজের সীমানা একটি সমবাহু ত্রিভুজের উপর ভিত্তি করে একটি ধ্রুবক প্রস্থ বক্ররেখা। একটি পাশের সমস্ত বিন্দু বিপরীত শীর্ষ থেকে সমান দূরত্বে অবস্থিত।

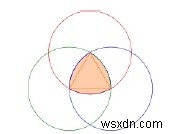
একটি Reuleaux ত্রিভুজ তৈরি করতে

Reuleaux ত্রিভুজের সূত্র

Reuleaux ত্রিভুজের ক্ষেত্রফল, যদি একটি সমবাহু ত্রিভুজের উপর ভিত্তি করে বক্ররেখা হয় এবং ত্রিভুজের বাহুর হয় h

A = (π * h2) / 2 – 2 * (Area of equilateral triangle) = (π – √3) * h2 / 2 = 0.70477 * h2

সবচেয়ে বড় রেউলক্স ত্রিভুজ একটি বর্গক্ষেত্রের মধ্যে খোদিত যা একটি উপবৃত্তের মধ্যে খোদাই করা আছে

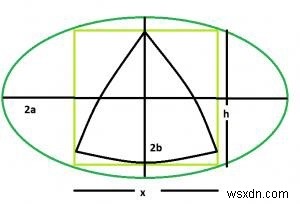
সবচেয়ে বড় রেউলক্স ত্রিভুজ একটি বর্গক্ষেত্রের মধ্যে খোদিত যা একটি উপবৃত্তের মধ্যে খোদাই করা আছে

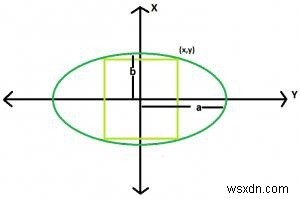
সবচেয়ে বড় বর্গক্ষেত্র যা একটি উপবৃত্তের মধ্যে খোদাই করা আছে

যদি একটি বর্গক্ষেত্র একটি উপবৃত্তে খোদাই করা হয়,

মাত্রাবৃত্তের সমীকরণ হল x^2/a^2 + y^2/b^2 =1

যদি, x =y

তারপর, x^2/a^2 + x^2/b^2 =1

তাই, x =√(a^2 + b^2)/ab

y =√(a^2 + b^2)/ab তারপর এলাকা, A =4(a^2 + b^2)/a^2b^2

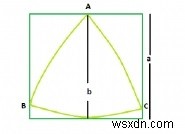
একটি বর্গক্ষেত্রের মধ্যে সবচেয়ে বড় রেউলক্স ত্রিভুজ

Reuleaux ত্রিভুজের ক্ষেত্রফল হল 0.70477 * b ² যেখানে b Reuleaux ত্রিভুজ সমর্থনকারী সমান্তরাল রেখাগুলির মধ্যে দূরত্ব।

Reuleaux ত্রিভুজকে সমর্থনকারী সমান্তরাল রেখার মধ্যে দূরত্ব =বর্গক্ষেত্রের বাহু অর্থাৎ a

রেউলক্স ত্রিভুজের ক্ষেত্রফল, A =0.70477 * a ²

একটি উদাহরণ নেওয়া যাক,

Input: a = 5, b = 4
Output: 0.0722389

ব্যাখ্যা

একটি উপবৃত্তের মধ্যে খোদাই করা বর্গক্ষেত্রের দিকটি হল, x =√(a^2 + b^2)/ab .

reuleaux ত্রিভুজ, h =x =√(a^2 + b^2)/ab .

রিউলক্স ত্রিভুজের ক্ষেত্রফল, A =0.70477*h^2 =0.70477*((a^2 + b^2)/a^2b^2) .

উদাহরণ

#include <stdio.h>
#include<math.h>
int main() {
   float a = 6, b = 8;
   float h = sqrt(((pow(a, 2) + pow(b, 2))/ (pow(a, 2) * pow(b, 2))));
   float area = 0.70477 * pow(h, 2);
   printf("The area is : %f", area);
   return 0;
}

আউটপুট

The area is : 0.030589