সবচেয়ে বড় রেউলক্স ত্রিভুজ একটি বর্গক্ষেত্রের মধ্যে খোদাই করা হয়েছে যা একটি উপবৃত্তের মধ্যে খোদাই করা আছে?

এখানে আমরা একটি বর্গক্ষেত্রের মধ্যে খোদাই করা বৃহত্তম রেউলক্স ত্রিভুজের ক্ষেত্রফল দেখব, সেই বর্গটি একটি উপবৃত্তের ভিতরে খোদাই করা আছে। আমরা জানি যে প্রধান অক্ষের দৈর্ঘ্য 2a, এবং ছোট অক্ষের দৈর্ঘ্য 2b। বর্গক্ষেত্রের দিকটি হল 'x', এবং Reuleaux ত্রিভুজের উচ্চতা হল h৷

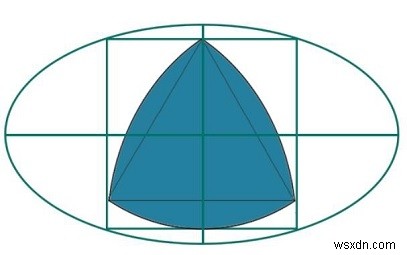
আমরা জানি যে প্রধান অক্ষ 2a এবং ছোট অক্ষ 2b সহ একটি উপবৃত্তে খোদাই করা একটি বর্গক্ষেত্রের দিক হল −

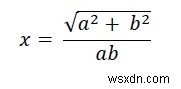
Reuleaux ত্রিভুজের উচ্চতা a এর সমান। তাই h =x. সুতরাং Reuleaux ত্রিভুজের ক্ষেত্রফল হল −

।

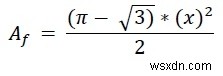উদাহরণ

#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float a, float b) { //a and b are half of major and minor axis of ellipse
   if (a < 0 || b < 0) //either a or b is negative it is invalid
      return -1;
   float x = sqrt((a*a) + (b*b)) / (a*b);
   float area = ((3.1415 - sqrt(3)) * (x) * (x))/2;
   return area;
}
int main() {
   float a = 5;
   float b = 4;
   cout << "Area of Reuleaux Triangle: " << areaReuleaux(a, b);
}

আউটপুট

Area of Reuleaux Triangle: 0.0722343