সংযোগ, দূরত্ব, এবং স্প্যানিং গাছ

স্প্যানিং ট্রি

একটি সহজ সংজ্ঞা হল যে একটি গাছ হল একটি সংযুক্ত গ্রাফ যা কোন চক্রের সাথে যুক্ত নয়, যেখানে একটি চক্র আমাদের একটি প্রান্তের পুনরাবৃত্তি না করে একটি নোড থেকে নিজের দিকে যেতে দেয়৷

একটি সংযুক্ত গ্রাফ G-এর জন্য একটি বিস্তৃত গাছকে G-এর সমস্ত শীর্ষবিন্দু রয়েছে এমন একটি গাছ হিসাবে সংজ্ঞায়িত করা হয়।

ইন্টারনেট রাউটিং অ্যালগরিদমের জন্য প্রায়ই স্প্যানিং ট্রি প্রয়োগ করা হয়। ইন্টারনেটে, কম্পিউটার (নোড) প্রায়ই অনেক অপ্রয়োজনীয় শারীরিক সংযোগের সাথে সংযুক্ত থাকে।

একটি গ্রাফে স্প্যানিং গাছের মোট সংখ্যা। যদি একটি গ্রাফ n নম্বর সহ একটি সম্পূর্ণ গ্রাফ হয়। শীর্ষবিন্দুর, তারপর বিস্তৃত গাছের মোট সংখ্যা হল n(n-2)

যেখানে n কে গ্রাফে নোডের সংখ্যা হিসাবে চিহ্নিত করা হয়। সম্পূর্ণ গ্রাফে, কাজটি এন নোড সহ বিভিন্ন লেবেলযুক্ত গাছ গণনা করার সমান যার জন্য কেলির সূত্র রয়েছে।

সংযোগ

গণিত এবং কম্পিউটার বিজ্ঞানে, সংযোগ গ্রাফ তত্ত্বের মৌলিক ধারণাগুলির মধ্যে একটি

এটির জন্য ন্যূনতম সংখ্যক উপাদানের (নোড বা প্রান্ত) প্রয়োজন যা অবশিষ্ট নোডগুলিকে বিচ্ছিন্ন সাবগ্রাফে আলাদা করার জন্য সরানো প্রয়োজন৷

এটি নেটওয়ার্ক প্রবাহ সমস্যার তত্ত্বের সাথে ঘনিষ্ঠভাবে সম্পর্কিত।

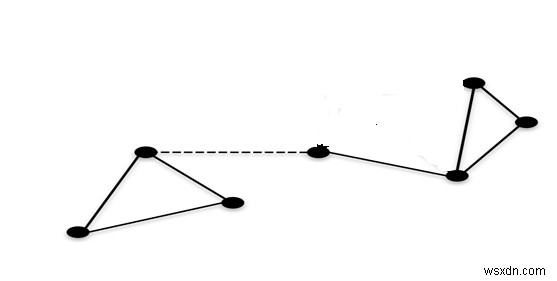
ড্যাশেড প্রান্তটি মুছে গেলে এই গ্রাফটি সংযোগ বিচ্ছিন্ন হয়ে যায়।

ভার্টেক্স সংযোগ। একটি গ্রাফের শীর্ষ সংযোগ হল কমপক্ষে সংখ্যক নোড যার মুছে ফেলার ফলে এটি সংযোগ বিচ্ছিন্ন হয়।

ভার্টেক্স সংযোগকে কখনও কখনও "পয়েন্ট সংযোগ" বা সহজভাবে "সংযোগ" হিসাবে চিহ্নিত করা হয়।

প্রান্ত সংযোগ. গ্রাফ থেকে সংযোগ বিচ্ছিন্ন হওয়া প্রান্তের অন্তত সংখ্যা, লাইন সংযোগ হিসাবেও চিহ্নিত।

একটি সংযোগ বিচ্ছিন্ন গ্রাফের প্রান্ত সংযোগ হল 0, যেখানে একটি গ্রাফ সেতুর সাথে যুক্ত একটি সংযুক্ত গ্রাফের হল 1৷

দূরত্ব

দুটি নোডের মধ্যে দূরত্ব সর্বনিম্ন সাধারণ পূর্বপুরুষের পরিপ্রেক্ষিতে গণনা করা যেতে পারে। সূত্রটি নিম্নরূপ।

Dist(d1, d2) = Dist(root, d1) + Dist(root, d2) - 2*Dist(root, lca)
'd1' and 'd2' are the two given keys
'root' is root of given Binary Tree.
'lca' is lowest common ancestor of d1 and d2
Dist(d1, d2) is the distance between d1 and d2.