গ্রাফ এবং এর ট্রাভার্সাল অ্যালগরিদম

এই বিভাগে আমরা গ্রাফ ডেটা স্ট্রাকচার কী এবং এর ট্রাভার্সাল অ্যালগরিদমগুলি দেখব৷

গ্রাফ হল একটি নন-লিনিয়ার ডেটা স্ট্রাকচার। এটি কিছু নোড এবং তাদের সংযুক্ত প্রান্ত নিয়ে গঠিত। প্রান্তগুলি পরিচালক বা অনির্দেশিত হতে পারে। এই গ্রাফটি G(V, E) হিসাবে উপস্থাপন করা যেতে পারে। নিম্নলিখিত গ্রাফটিকে G({A, B, C, D, E}, {(A, B), (B, D), (D, E), (B, C), (C, A) হিসাবে উপস্থাপন করা যেতে পারে )})

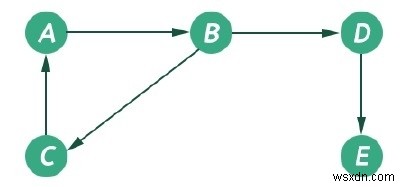
গ্রাফটিতে দুই ধরনের ট্রাভার্সাল অ্যালগরিদম রয়েছে। এগুলোকে বলা হয় ব্রেডথ ফার্স্ট সার্চ এবং ডেপথ ফার্স্ট সার্চ।

ব্রেডথ ফার্স্ট সার্চ (BFS)

ব্রেডথ ফার্স্ট সার্চ (BFS) ট্রাভার্সাল হল একটি অ্যালগরিদম, যা একটি প্রদত্ত গ্রাফের সমস্ত নোড দেখার জন্য ব্যবহৃত হয়। এই ট্রাভার্সাল অ্যালগরিদমে একটি নোড নির্বাচন করা হয় এবং তারপরে পার্শ্ববর্তী সমস্ত নোডগুলি একে একে পরিদর্শন করা হয়। সমস্ত সংলগ্ন শীর্ষবিন্দুগুলি সম্পূর্ণ করার পরে, এটি অন্য শীর্ষবিন্দুগুলি পরীক্ষা করার জন্য আরও এগিয়ে যায় এবং এর সন্নিহিত শীর্ষগুলি আবার পরীক্ষা করে৷

অ্যালগরিদম

bfs(vertices, start)
Input: The list of vertices, and the start vertex.
Output: Traverse all of the nodes, if the graph is connected.
Begin
   define an empty queue que
   at first mark all nodes status as unvisited
   add the start vertex into the que
   while que is not empty, do
      delete item from que and set to u
      display the vertex u
      for all vertices 1 adjacent with u, do
         if vertices[i] is unvisited, then
            mark vertices[i] as temporarily visited
            add v into the queue
         mark
      done
      mark u as completely visited
   done
End

গভীর প্রথম অনুসন্ধান (DFS)

ডেপথ ফার্স্ট সার্চ (DFS) হল একটি গ্রাফ ট্রাভার্সাল অ্যালগরিদম। এই অ্যালগরিদমে একটি প্রারম্ভিক শীর্ষবিন্দু দেওয়া হয়, এবং যখন একটি সংলগ্ন শীর্ষবিন্দু পাওয়া যায়, এটি প্রথমে সেই সন্নিহিত শীর্ষে চলে যায় এবং একই পদ্ধতিতে অতিক্রম করার চেষ্টা করে৷

অ্যালগরিদম

dfs(vertices, start)
Input: The list of all vertices, and the start node.
Output: Traverse all nodes in the graph.
Begin
   initially make the state to unvisited for all nodes
   push start into the stack
   while stack is not empty, do
      pop element from stack and set to u
      display the node u
      if u is not visited, then
         mark u as visited
         for all nodes i connected to u, do
            if ith vertex is unvisited, then
               push ith vertex into the stack
               mark ith vertex as visited
         done
   done
End