এই বিভাগে আমরা একটি বাইনারি ট্রি ডেটা স্ট্রাকচারের কিছু গুরুত্বপূর্ণ বৈশিষ্ট্য দেখব। ধরুন আমাদের এরকম একটি বাইনারি গাছ আছে।
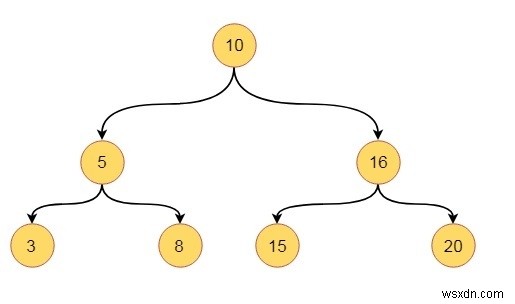
কিছু বৈশিষ্ট্য হল −
- লেভেল 'l' এ নোডের সর্বোচ্চ সংখ্যা হবে $2^{l-1}$। এখানে স্তর হল রুট থেকে নোডে যাওয়ার পথে নোডের সংখ্যা, রুটটি সহ। আমরা বিবেচনা করছি রুটের স্তর হল 1।
- h উচ্চতার বাইনারি ট্রিতে উপস্থিত নোডের সর্বাধিক সংখ্যা হল $2^{h}-1$। এখানে উচ্চতা হল রুট থেকে পাতা পর্যন্ত নোডের সর্বোচ্চ সংখ্যা। এখানে আমরা একটি নোড সহ একটি গাছের উচ্চতা বিবেচনা করছি 1।
- n নোড সহ একটি বাইনারি ট্রিতে, ন্যূনতম সম্ভাব্য উচ্চতা বা সর্বনিম্ন সংখ্যক স্তর হল$\log_{2}\lgroup{n+1}\rgroup$। যদি আমরা বিবেচনা করি যে লিফ নোডের উচ্চতা 0 হিসাবে বিবেচিত হয়, তাহলে সূত্রটি হবে $\log_{2}\lgroup{n+1}\rgroup-1$
- 'L' পাতা সহ একটি বাইনারি গাছে কমপক্ষে $\log_{2}{L+1}$ সংখ্যক স্তর থাকে
- যদি একটি বাইনারি গাছের 0 বা 2টি সন্তান থাকে, তাহলে পাতার নোডের সংখ্যা সবসময় দুটি সন্তানের নোডের চেয়ে এক বেশি হয়৷
N.B. বাইনারি গাছ যেমন এক ধরনের গাছ; গ্রাফ তত্ত্বে এটিতে গাছের সমস্ত বৈশিষ্ট্য রয়েছে।


