মেল্ডেবল অগ্রাধিকার সারি
সংজ্ঞা
একটি র্যান্ডমাইজড মেল্ডেবল হিপ (এছাড়াও মেলডেবল হিপ বা র্যান্ডমাইজড মেল্ডেবল অগ্রাধিকার সারি) একটি অগ্রাধিকার সারি ভিত্তিক ডেটা কাঠামো হিসাবে সংজ্ঞায়িত করা হয় যেখানে অন্তর্নিহিত কাঠামোটিও একটি হিপ-অর্ডার বাইনারি ট্রি। যাইহোক, অন্তর্নিহিত বাইনারি গাছের আকারের উপর কোন কঠিন এবং দ্রুত নিয়ম নেই।
সুবিধা
- এই পদ্ধতির অনেকগুলি সুবিধা রয়েছে যেমন অনুরূপ ডেটা স্ট্রাকচারের উপর সুবিধা।
- এটি অন্যান্য ডেটা স্ট্রাকচারের তুলনায় সহজ পদ্ধতির প্রস্তাব করে।
- এলোমেলোভাবে মেলেডেবল হিপের জন্য সমস্ত ক্রিয়াকলাপ প্রয়োগ করা সহজ এবং তাদের জটিলতার সীমার ধ্রুবক কারণগুলি ছোট৷
- এছাড়াও ভারসাম্য রক্ষার কোনো প্রয়োজন নেই এবং নোডের মধ্যে কোনো স্যাটেলাইট তথ্যের প্রয়োজন নেই।
- অবশেষে, এই কাঠামোটি সবচেয়ে খারাপ ক্ষেত্রে সময় দক্ষতা প্রদর্শন করে। সাধারণত প্রতিটি পৃথক অপারেশনের কার্যকর করার সময় উচ্চ সম্ভাবনার সাথে লগারিদমিক হয়।
Skew Heaps
একটি স্কু হিপ (বা স্ব-অ্যাডজাস্টিং হিপ) একটি হিপ ডেটা স্ট্রাকচার হিসাবে সংজ্ঞায়িত করা হয় যা একটি বাইনারি ট্রি হিসাবে প্রয়োগ করা হয়৷
স্কু হিপগুলি সুবিধাজনক কারণ তারা বাইনারি হিপগুলির তুলনায় আরও দ্রুত একত্রিত হতে পারে৷
বাইনারি স্তূপগুলির বিপরীতে, কোনও কাঠামোগত সীমাবদ্ধতা নেই, তাই গাছের উচ্চতা লগারিদমিক হওয়ার কোনও গ্যারান্টি নেই৷
শুধুমাত্র দুটি শর্ত অবশ্যই সন্তুষ্ট হতে হবে -
- সাধারণ হিপ অর্ডার অবশ্যই সেখানে বজায় রাখতে হবে (মূল ন্যূনতম এবং একই সাবট্রির জন্য পুনরাবৃত্তভাবে সত্য), তবে সুষম সম্পত্তি (সর্বশেষ ব্যতীত সমস্ত স্তর অবশ্যই পূর্ণ হতে হবে) প্রয়োজন নেই৷
- Skew Heaps-এ প্রধান অপারেশন শুধুমাত্র মার্জ। আমরা শুধুমাত্র মার্জ এর সাথে যুক্ত ইনসার্ট, এক্সট্রাক্টমিন(), ইত্যাদির মত অন্যান্য ক্রিয়াকলাপ বাস্তবায়ন করতে পারি।
উদাহরণ
স্কু হিপ 1 হতে দিন

দ্বিতীয় হিপটি ধরে নেওয়া হবে
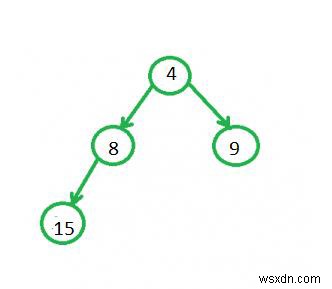
এবং আমরা চূড়ান্ত একত্রিত গাছটি
আকারে পাই
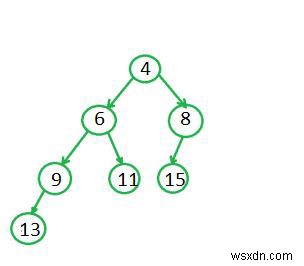
পুনরাবৃত্ত মার্জ প্রক্রিয়া
merge(a1, a2)একত্রিত করার জন্য a1 এবং a2 দুটি মিনিট স্কু হিপস হতে দিন। a1 এর রুট a2 এর রুট থেকে ছোট হোক (যদি ছোট না হয়, আমরা একই পেতে অদলবদল করতে পারি। প্রাক>


