এই বিভাগে আমরা ইউলারিয়ান এবং হ্যামিলটোনিয়ান গ্রাফগুলি দেখতে পাব। তবে এর মধ্যে ডুব দেওয়ার আগে, প্রথমে আমাদের গ্রাফে ট্রেইলগুলি কী তা দেখতে হবে। ধরুন আমাদের নিচের মত একটি গ্রাফ আছে −
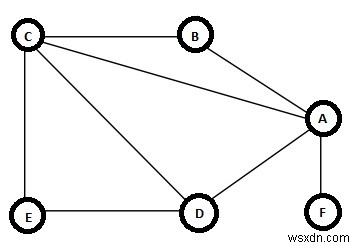
ট্রেইল হল একটি পথ, যা কিনারাগুলির একটি ক্রম (v1, v2), (v2, v3), …, (vk - 1, vk) যেখানে সমস্ত শীর্ষবিন্দু (v1, v2, … , vk) আলাদা নাও হতে পারে , কিন্তু সব প্রান্ত আলাদা। এই উদাহরণে একটি ট্রেইল হল {(B, A), (A, C), (C, D), (D, A), (A, F)} এটি একটি ট্রেইল। কিন্তু এটিকে সহজ পথ হিসাবে বিবেচনা করা হবে না কারণ শীর্ষবিন্দু A দুবার পরিদর্শন করা হয়েছে। যদি প্রথম এবং শেষ শীর্ষবিন্দু একই হয়, তাহলে সেটি হবে একটি বন্ধ পথ।
ইউলেরিয়ান ট্রেইল
G(V, E) একটি গ্রাফে ইউলেরিয়ান ট্রেইল হল একটি ট্রেইল, যেটিতে প্রতিটি প্রান্ত ঠিক একবার অন্তর্ভুক্ত থাকে। G যদি ইউলারিয়ান ট্রেইল বন্ধ করে থাকে, তাহলে সেই গ্রাফটিকে ইউলারিয়ান গ্রাফ বলা হয়। অন্য কথায়, আমরা বলতে পারি যে একটি গ্রাফ G হবে ইউলারিয়ান গ্রাফ, যদি একটি শীর্ষবিন্দু থেকে শুরু হয়, আমরা প্রতিটি প্রান্ত ঠিক একবার অতিক্রম করতে পারি এবং প্রারম্ভিক শীর্ষে ফিরে যেতে পারি। অয়লার প্রমাণ করেছেন যে একটি গ্রাফকে ইউলারিয়ান গ্রাফ বলা হয় যদি এবং শুধুমাত্র যদি এর প্রতিটি শীর্ষবিন্দুর মাত্রা সমান হয়।
হ্যামিল্টোনিয়ান সাইকেল
একটি চক্রকে হ্যামিলটোনিয়ান চক্র বলা হয় যদি এটি গ্রাফ G এর প্রতিটি শীর্ষের মধ্য দিয়ে যায়। অনেকগুলি বিভিন্ন উপপাদ্য রয়েছে যা একটি গ্রাফকে হ্যামিলটোনিয়ান হওয়ার জন্য যথেষ্ট শর্ত দেয়। যাইহোক, একটি নির্বিচারে গ্রাফ হ্যামিলটোনিয়ান কিনা তা নির্ধারণ করতে সমস্যা হল NPCসম্পূর্ণ সমস্যা।


