ডেটা স্ট্রাকচারে অভিযোজিত মার্জিং এবং বাছাই

অ্যাডাপ্টিভ মার্জ সর্ট

অ্যাডাপটিভ মার্জ সর্ট সাজানো সাব-লিস্ট মার্জ সাজানোর কাজ করে। যাইহোক, প্রাথমিক সাব-লিস্টের আকার 1 আকারের উপ-তালিকা না থাকার পরিবর্তে উপাদানগুলির তালিকার মধ্যে অর্ডার করার অস্তিত্বের উপর নির্ভর করে। উদাহরণস্বরূপ, চিত্রে তালিকা বিবেচনা করুন।

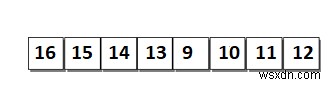
এটি 2টি সাজানো উপ-তালিকা নিয়ে গঠিত৷

• 16,15,14,13 উপাদান সহ উপ-তালিকা 1।
• 9,10,11,12 উপাদান সহ উপ-তালিকা 2।

সাব-লিস্ট 1 সাজানো হয়েছে কিন্তু বিপরীত ক্রমে। এইভাবে, উপ-তালিকা 1 চিত্রে দেখানো হিসাবে বিপরীত হয়।

সাব-তালিকা পাওয়া গেলে মার্জিং প্রক্রিয়া শুরু হয়। অভিযোজিত মার্জ বাছাই সাব-তালিকাগুলিকে একত্রিত করা শুরু করে। অভিযোজিত মার্জ সাজানোর জন্য শুধুমাত্র একটি মার্জিং ধাপের প্রয়োজন হবে কারণ শুধুমাত্র 2টি উপ-তালিকা রয়েছে। মার্জ করার ফলাফল চিত্রে দেখানো হয়েছে৷

ডিজাইন আইডিয়া

• সাব-তালিকাগুলি খুঁজে বের করে শুরু করুন যা ইতিমধ্যেই প্রয়োজনীয় বা বিপরীত ক্রমে সাজানো হয়েছে
• যদি বিপরীত ক্রমে উপাদান সহ কোনো উপ-তালিকা বিদ্যমান থাকে, তাহলে সাব-তালিকাটিকে উলটো করে ১ম এলিমেন্টকে শেষের সাথে, ২য় এলিমেন্টকে ২য় শেষের সাথে পরিবর্তন করে এটি চালিয়ে যেতে হবে।
• নতুন উপ-তালিকা তৈরি করতে উপ-তালিকাগুলিকে একত্রিত করতে থাকুন যতক্ষণ না শুধুমাত্র 1টি উপ-তালিকা অবশিষ্ট থাকে।

অ্যাডাপ্টিভ মার্জ বাছাই বিশ্লেষণ

অভিযোজিত মার্জ সাজানোর পরিবর্তে সাইজ 1 এর সাব-তালিকা দিয়ে শুরু করে, একটি উপ-তালিকা খুঁজে পায় যা ইতিমধ্যেই প্রয়োজনীয় বা বিপরীত ক্রমে সাজানো আছে। প্রাথমিকভাবে পাওয়া সাব-লিস্টের আকার হবে সর্বনিম্ন 2 এবং সর্বোচ্চ m (m হল উপাদানের সংখ্যা)।

যাইহোক, যদি সাব-লিস্টে বিপরীত ক্রমে উপাদান থাকে, তাহলে এটি একটি মার্জ অপারেশন শুরু করার আগে তালিকাটিকে বিপরীত করে দেয়। তালিকা উল্টানোর জন্য (m/2) বিনিময় ক্রিয়াকলাপ প্রয়োজন৷

সেরা কেস

যদি তালিকাটি ইতিমধ্যেই সাজানো ক্রমে বা বিপরীত ক্রমে থাকে, তাহলে অভিযোজিত একত্রীকরণ সাজানোর শুধুমাত্র একটি তালিকা থাকবে এবং এর জন্য কোনো মার্জ অপারেশনের প্রয়োজন হবে না। যাইহোক, তালিকাটি ইতিমধ্যেই সাজানো হয়েছে তা খুঁজে বের করার জন্য O(m) তুলনা অপারেশন এবং (m/2) বিনিময় অপারেশন প্রয়োজন হবে যদি তালিকাটি বিপরীত ক্রমে সাজানো হয়। এটি অ্যাডাপ্টিভ মার্জ সর্টকে অভিযোজিত করে তোলে এমনকি যখন তালিকাটি বিপরীত ক্রমে সাজানো হয়।

এইভাবে সেরা ক্ষেত্রের জন্য সময় জটিলতা নিম্নরূপ গণনা করা হয় -

T(m) = (m-1)+(m/2)
T(m) = (2m-2+m)/2
T(m) = O(m).

যাইহোক, অ্যাডাপ্টিভ মার্জ সর্ট মার্জ সাজানোর তুলনায় O(m) এর অতিরিক্ত স্থান প্রয়োগ করে

সবচেয়ে খারাপ কেস

অভিযোজিত মার্জ বাছাই সাব-তালিকা খুঁজে পাবে যা ইতিমধ্যে প্রয়োজনীয় বা বিপরীত ক্রমে সাজানো হয়েছে। যাইহোক, সবচেয়ে খারাপ ক্ষেত্রে কোন আংশিক বা মোট অর্ডার উপাদান নেই। এইভাবে, প্রাথমিকভাবে পাওয়া সাব-তালিকাটি আকার 2 হবে। একবার সাব-তালিকা পাওয়া গেলে মার্জিং প্রক্রিয়া শুরু হয়।

• আকার 2-এর উপ-তালিকা একত্রিত করার ফলে আকার 4-এর সাজানো উপ-তালিকা পাওয়া যায়।
• আকার 4 এর সাব-তালিকা একত্রিত করার ফলে 8 আকারের সাব-লিস্ট সাজানো হয়।
• একত্রীকরণ প্রক্রিয়া 2k <মি না হওয়া পর্যন্ত চলতে থাকে। যেখানে k হল kth মার্জিং ধাপ।

যেহেতু অ্যাডাপ্টিভ মার্জ সাজানোর সবচেয়ে খারাপ ক্ষেত্রে মার্জ করার ধাপগুলি মার্জ সাজানোর মতোই। সুতরাং, অভিযোজিত মার্জ সাজানোর সবচেয়ে খারাপ ক্ষেত্রে সময়ের জটিলতা একত্রিতকরণের মতোই-

T(m) = O(m log m).