এখানে আমরা দেখব কিভাবে একটি n-পার্শ্বযুক্ত নিয়মিত বহুভুজের ক্ষেত্রফল পাওয়া যায় যার ব্যাসার্ধ দেওয়া আছে। এখানে ব্যাসার্ধ হল যেকোনো শীর্ষবিন্দুর কেন্দ্র থেকে দূরত্ব। এই সমস্যাটি সমাধান করার জন্য, আমরা কেন্দ্র থেকে একপাশে একটি লম্ব আঁকলাম। প্রতিটি পাশ দৈর্ঘ্য 'a' হয়। লম্ব দিকটিকে দুই ভাগে ভাগ করছে। প্রতিটি অংশের দৈর্ঘ্য a/2। লম্ব এবং একটি ব্যাসার্ধ একটি কোণ x তৈরি করছে। ধরা যাক ব্যাসার্ধের দৈর্ঘ্য h।
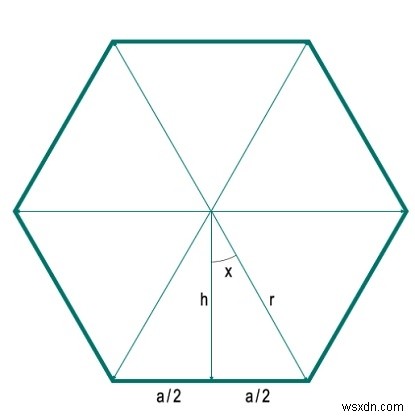
এখানে আমরা দেখতে পাচ্ছি যে বহুভুজটি N সমান ত্রিভুজে বিভক্ত। সুতরাং N বাহুর যেকোনো বহুভুজের জন্য, N ত্রিভুজে বিভক্ত হবে। সুতরাং কেন্দ্রে কোণ হল 360। এটি 360°/N বিভিন্ন কোণে বিভক্ত (এখানে 360°/6 =60°)। সুতরাং কোণ x হল 180°/N। এখন আমরা ত্রিকোণমিতিক সমীকরণ ব্যবহার করে সহজেই h এবং a পেতে পারি।
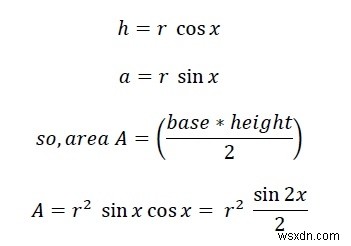
এখন পুরো বহুভুজের ক্ষেত্রফল হল N*A.
উদাহরণ
#include <iostream>
#include <cmath>
using namespace std;
float polygonArea(float r, int n){
return ((r * r * n) * sin((360 / n) * 3.1415 / 180)) / 2; //convert
angle to rad then calculate
}
int main() {
float rad = 9.0f;
int sides = 6;
cout << "Polygon Area: " << polygonArea(rad, sides);
} আউটপুট
Polygon Area: 210.44


