একটি প্রদত্ত বাহুর সাথে একটি এন-পার্শ্বযুক্ত নিয়মিত বহুভুজের ক্ষেত্রফল খুঁজে বের করার এই সমস্যায়, আমরা চিত্রটির ক্ষেত্রফলের সূত্রটি বের করব এবং এর উপর ভিত্তি করে একটি প্রোগ্রাম তৈরি করব। কিন্তু তার আগে চলুন বিষয়টা সহজে বোঝার জন্য মৌলিক বিষয়গুলো পর্যালোচনা করি।
একটি N-পার্শ্বযুক্ত নিয়মিত বহুভুজ n বাহুর একটি বহুভুজ যার সব বাহু সমান। যেমন রেগুলার পেন্টাগন, রেগুলার হেক্সাগন, ইত্যাদি।
এলাকা কোনো দ্বি-মাত্রিক চিত্রের পরিমাণের পরিমাণগত উপস্থাপনা।
এই চিত্রটির ক্ষেত্রফল বের করার জন্য আমাদের চিত্রটিতে পৃথক ত্রিভুজের ক্ষেত্রফল খুঁজে বের করতে হবে এবং এটির বাহুর সংখ্যা দিয়ে গুণ করতে হবে। যেহেতু আমরা এন সাইডেড।
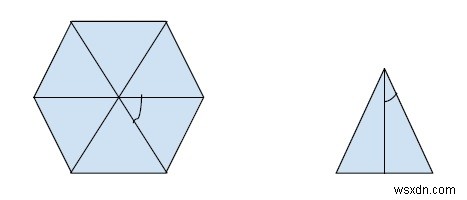
এখন, উপরের চিত্র থেকে, আমরা এলাকার জন্য একটি সূত্র তৈরি করতে পারি।
নিয়মিত বহুভুজের প্রতিটি বাহু একটি ত্রিভুজ বাহুর a (বহুভুজের পার্শ্ব) এবং কোণ 180 / n তৈরি করতে পারে (n হল একটি বহুভুজের বাহুর সংখ্যা)। সুতরাং, সূত্র ব্যবহার করে এলাকাটি পাওয়া যাবে,
ত্রিভুজের ক্ষেত্রফল =½ * b * h
এখন, h =a * tan(180/n)
So , area = ½ * a * a / 2 * tan(180/n) = a * a / (4 * tan(180/n))
বহুভুজের একটি পৃথক ত্রিভুজের জন্য এই সূত্রটি ব্যবহার করে, আমরা পুরো বহুভুজের ক্ষেত্রফল তৈরি করতে পারি,
n-পার্শ্বযুক্ত নিয়মিত বহুভুজের ক্ষেত্রফল =n * (a * a / (4 * tan(180 /n)))
অ্যালগরিদম
Step 1 : calculate the value of angle using (180 / n) Step 2 : Calculate the area of regular polygon using n * (a * a / (4 * tan(180 /n))) . Step 3 : Print the area of polygon.
উদাহরণ
#include<iostream>
#include<math.h>
using namespace std;
int main(){
float a = 12, n = 9;
float area=(a * a * n) / (4 * tan((180 / n) * 3.14159 / 180));
cout<<"The area of "<<n<<" sided regular polygon of side "<<a<<" is "<<area;
return 0;
} আউটপুট
The area of 9 sided regular polygon of side 12 is 890.183


