অয়লার পথ একটি পথ; যার মাধ্যমে আমরা প্রতিটি নোড একবার দেখতে পারি। আমরা একই প্রান্ত একাধিকবার ব্যবহার করতে পারি। অয়লার সার্কিট হল একটি বিশেষ ধরনের অয়লার পাথ। যখন অয়লার পথের প্রারম্ভিক শীর্ষবিন্দুও সেই পথের শেষ শীর্ষের সাথে সংযুক্ত থাকে।
অয়লার পাথ সনাক্ত করতে, আমাদের এই শর্তগুলি অনুসরণ করতে হবে
- গ্রাফটি অবশ্যই সংযুক্ত থাকতে হবে।
- এখন যখন একটি অনির্দেশিত গ্রাফের কোনো শীর্ষবিন্দুর বিজোড় ডিগ্রি নেই, তখন এটি একটি অয়লার সার্কিট, যা একটি অয়লার পথও।
- যখন ঠিক দুটি শীর্ষবিন্দুর বিজোড় ডিগ্রি থাকে, তখন এটি একটি অয়লার পাথ৷
ইনপুট
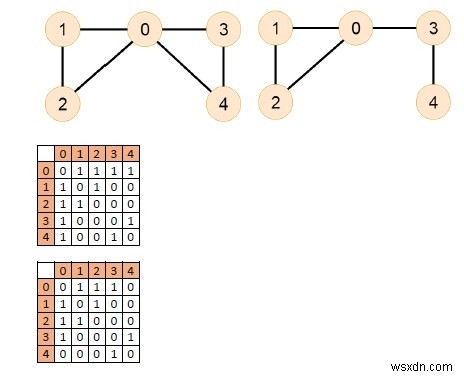
আউটপুট
উভয় গ্রাফেই অয়লার পাথ রয়েছে।
অ্যালগরিদম
ট্রাভার্স(u, পরিদর্শন করা)
ইনপুট:কোন নোডটি পরিদর্শন করা হয়েছে তা চিহ্নিত করতে স্টার্ট নোড u এবং ভিজিট করা নোড।
আউটপুট:সমস্ত সংযুক্ত শীর্ষবিন্দু অতিক্রম করুন।
Begin mark u as visited for all vertex v, if it is adjacent with u, do if v is not visited, then traverse(v, visited) done End
সংযুক্ত (গ্রাফ)
ইনপুট:গ্রাফ।
আউটপুট:গ্রাফ সংযুক্ত থাকলে সত্য।
Begin define visited array for all vertices u in the graph, do make all nodes unvisited traverse(u, visited) if any unvisited node is still remaining, then return false done return true End
isEulerian(গ্রাফ)
ইনপুট:প্রদত্ত গ্রাফ।
আউটপুট:ইউলারিয়ান সার্কিট বা পাথ হলে 1 রিটার্ন করে এবং অয়লার পাথ না থাকলে 0 রিটার্ন করে।
Begin if isConnected() is false, then return false define list of degree for each node oddDegree := 0 for all vertex i in the graph, do for all vertex j which are connected with i, do increase degree done if degree of vertex i is odd, then increase oddDegree done if oddDegree > 0, then return 0 else return 1 End
উদাহরণ কোড
#include<iostream>
#include<vector>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {{0, 1, 1, 1, 0},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{1, 0, 0, 0, 1},
{0, 0, 0, 1, 0}};
/*int graph[NODE][NODE] = {{0, 1, 1, 1, 1},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{1, 0, 0, 0, 1},
{1, 0, 0, 1, 0}};*/ //uncomment to check Euler Circuit as well as path
/*int graph[NODE][NODE] = {{0, 1, 1, 1, 0},
{1, 0, 1, 1, 0},
{1, 1, 0, 0, 0},
{1, 1, 0, 0, 1},
{0, 0, 0, 1, 0}};*/ //Uncomment to check Non Eulerian Graph
void traverse(int u, bool visited[]) {
visited[u] = true; //mark v as visited
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) {
if(!visited[v])
traverse(v, visited);
}
}
}
bool isConnected() {
bool *vis = new bool[NODE];
//for all vertex u as start point, check whether all nodes are visible or not
for(int u; u < NODE; u++) {
for(int i = 0; i<NODE; i++)
vis[i] = false; //initialize as no node is visited
traverse(u, vis);
for(int i = 0; i<NODE; i++){
if(!vis[i]) //if there is a node, not visited by traversal, graph is not connected
return false;
}
}
return true;
}
int isEulerian() {
if(isConnected() == false) //when graph is not connected
return 0;
vector<int> degree(NODE, 0);
int oddDegree = 0;
for(int i = 0; i<NODE; i++) {
for(int j = 0; j<NODE; j++) {
if(graph[i][j])
degree[i]++; //increase degree, when connected edge found
}
if(degree[i] % 2 != 0) //when degree of vertices are odd
oddDegree++; //count odd degree vertices
}
if(oddDegree > 2) //when vertices with odd degree greater than 2
return 0;
return 1; //when oddDegree is 0, it is Euler circuit, and when 2, it is Euler path
}
int main() {
if(isEulerian() != 0) {
cout << "The graph has Eulerian path." << endl;
} else {
cout << "The graph has No Eulerian path." << endl;
}
} আউটপুট
The graph has Eulerian path.


