একটি গ্রাফের সংযোগ পরীক্ষা করতে, আমরা যেকোনো ট্রাভার্সাল অ্যালগরিদম ব্যবহার করে সমস্ত নোড অতিক্রম করার চেষ্টা করব। ট্রাভার্সাল শেষ করার পর, যদি কোনো নোড থাকে, যা পরিদর্শন করা হয়নি, তাহলে গ্রাফটি সংযুক্ত নয়।
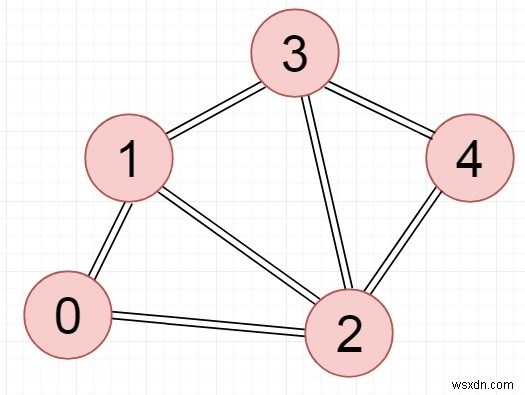
অনির্দেশিত গ্রাফের জন্য, আমরা একটি নোড নির্বাচন করব এবং এটি থেকে অতিক্রম করব।
এই ক্ষেত্রে ট্রাভার্সাল অ্যালগরিদম হল রিকার্সিভ BFS ট্রাভার্সাল৷
ইনপুট − একটি গ্রাফের সংলগ্নতা ম্যাট্রিক্স
| 0 | 1 | ৷1 | ৷0 | 0 |
| 1 | 0 | 1 | ৷1 | ৷0 |
| 1 | 1 | ৷0 | 1 | ৷1 | ৷
| 0 | 1 | ৷1 | ৷0 | 1 | ৷
| 0 | 0 | 1 | ৷1 | ৷0 |
আউটপুট − গ্রাফটি সংযুক্ত৷
৷অ্যালগরিদম
ট্রাভার্স (গুলি, পরিদর্শন করা)
৷ইনপুট − কোন নোডটি পরিদর্শন করা হয়েছে তা চিহ্নিত করতে স্টার্ট নোড এবং ভিজিট করা নোড।
আউটপুট − সমস্ত সংযুক্ত শীর্ষবিন্দু অতিক্রম করুন৷
৷Begin
mark s as visited
insert s into a queue Q
until the Q is not empty, do
u = node that is taken out from the queue
for each node v of the graph, do
if the u and v are connected, then
if u is not visited, then
mark u as visited
insert u into the queue Q.
done
done
End সংযুক্ত (গ্রাফ)
ইনপুট - গ্রাফ।
আউটপুট − গ্রাফটি সংযুক্ত থাকলে সত্য৷
৷Begin
define visited array
for all vertices u in the graph, do
make all nodes unvisited
traverse(u, visited)
if any unvisited node is still remaining, then
return false
done
return true
End উদাহরণ কোড (C++)
#include<iostream>
#include<queue>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 1, 0, 0},
{1, 0, 1, 1, 0},
{1, 1, 0, 1, 1},
{0, 1, 1, 0, 1},
{0, 0, 1, 1, 0}};
void traverse(int s, bool visited[]) {
visited[s] = true; //mark v as visited
queue<int> que;
que.push(s);//insert s into queue
while(!que.empty()) {
int u = que.front(); //delete from queue and print
que.pop();
for(int i = 0; i < NODE; i++) {
if(graph[i][u]) {
//when the node is non-visited
if(!visited[i]) {
visited[i] = true;
que.push(i);
}
}
}
}
}
bool isConnected() {
bool *vis = new bool[NODE];
//for all vertex u as start point, check whether all nodes are visible or not
for(int u; u < NODE; u++) {
for(int i = 0; i < NODE; i++)
vis[i] = false; //initialize as no node is visited
traverse(u, vis);
for(int i = 0; i < NODE; i++) {
if(!vis[i]) //if there is a node, not visited by traversal, graph is not connected
return false;
}
}
return true;
}
int main() {
if(isConnected())
cout << "The Graph is connected.";
else
cout << "The Graph is not connected.";
} আউটপুট
The Graph is connected.


