ডিফারেনশিয়াল সমীকরণের জন্য Runge-Kutta 4র্থ ক্রম নিয়ম

Runge Kutta পদ্ধতিটি সাধারণ ডিফারেনশিয়াল সমীকরণ (ODE) সমাধানের জন্য ব্যবহৃত হয়। এটি x এবং y-এর জন্য dy/dx ফাংশন ব্যবহার করে এবং y এর প্রাথমিক মানও প্রয়োজন, যেমন y(0)। এটি প্রদত্ত x এর জন্য y এর আনুমানিক মান খুঁজে পায়। ODE সমাধানের জন্য, আমাদের এই সূত্রগুলি অনুসরণ করতে হবে:

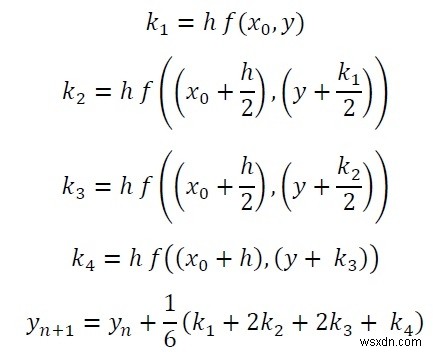
এখানে h হল ব্যবধানের উচ্চতা৷

দ্রষ্টব্য: এই সূত্রগুলি থেকে, আমরা প্রথম দুটি k1 এবং k2 ব্যবহার করে ODE-এর জন্য Runge-Kutta 2nd অর্ডার সমাধান খুঁজে পেতে পারি।

ইনপুট এবং আউটপুট

Input:
The x0 and f(x0): 0 and 0
the value of x = 0.4
the value of h = 0.1
Output:
Answer of differential equation: 0.0213594

অ্যালগরিদম

rungeKutta(x0, y0, x, h)

ইনপুট −৷ প্রারম্ভিক x এবং y মান, লক্ষ্য করা x মান, এবং ব্যবধানের উচ্চতা h।

আউটপুট − x মানের জন্য y এর মান।

Begin
   iteration := (x – x0)/h
   y = y0
   for i := 1 to iteration, do
      k1 := h*f(x0, y)
      k2 := h*f((x0 + h/2), (y + k1/2))
      k3 := h*f((x0 + h/2), (y + k2/2))
      k4 := h*f((x0 + h), (y + k3))
      y := y + (1/6)*(k1 + 2k2 + 2k3 + k4)
      x0 := x0 + h
   done
   return y
End

উদাহরণ

#include <iostream>
using namespace std;

double diffOfy(double x, double y) {
   return ((x*x)+(y*y)); //function x^2 + y^2
}

double rk4thOrder(double x0, double y0, double x, double h) {
   int iteration = int((x - x0)/h);    //calculate number of iterations
   double k1, k2, k3, k4;
   double y = y0;    //initially y is f(x0)

   for(int i = 1; i<=iteration; i++) {
      k1 = h*diffOfy(x0, y);
      k2 = h*diffOfy((x0+h/2), (y+k1/2));
      k3 = h*diffOfy((x0+h/2), (y+k2/2));
      k4 = h*diffOfy((x0+h), (y+k3));
         
      y += double((1.0/6.0)*(k1+2*k2+2*k3+k4));    //update y using del y
      x0 += h;    //update x0 by h
   }
   return y;    //f(x) value
}

int main() {
   double x0, y0, x, h;
   cout << "Enter x0 and f(x0): "; cin >> x0 >> y0;
   cout << "Enter x: "; cin >> x;
   cout << "Enter h: "; cin >> h;
   cout << "Answer of differential equation: " << rk4thOrder(x0, y0, x, h);
}

আউটপুট

Enter x0 and f(x0): 0 0
Enter x: 0.4
Enter h: 0.1
Answer of differential equation: 0.0213594