সুনির্দিষ্ট অবিচ্ছেদ্য জন্য সিম্পসনের 1/3 নিয়ম

ট্র্যাপিজয়েডাল নিয়মের মতো, সিম্পসনের 1/3য় নিয়মটিও a থেকে b পর্যন্ত সীমার অবিচ্ছেদ্য মান খুঁজে বের করতে ব্যবহৃত হয়। ট্র্যাপিজয়েডাল এবং সিম্পসনের 1/3য় নিয়মের মধ্যে প্রধান পার্থক্য হল, ট্র্যাপিজয়েডাল নিয়মে, পুরো বিভাগগুলিকে কিছু ট্র্যাপিজয়েডে বিভক্ত করা হয়, তবে এই ক্ষেত্রে, প্রতিটি ট্র্যাপিজয়েড দুটি ভাগে বিভক্ত।

এই নিয়মের জন্য, আমরা এই সূত্রটি অনুসরণ করব:

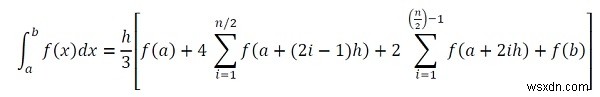
এখানে h হল ব্যবধানের প্রস্থ, এবং n হল অন্তরের সংখ্যা। আমরা

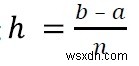
ইনপুট এবং আউটপুট

Input:
The function f(x): (x+(1/x). The lower and upper limit: 1, 2. The number of intervals: 20.
Output:
The answer is: 2.19315

অ্যালগরিদম

integrateSimpson(a, b, n)

ইনপুট - অখণ্ডের নিম্ন এবং উপরের সীমা এবং ব্যবধানের সংখ্যা n.

আউটপুট - একীকরণের পরে ফলাফল।

Begin
   h := (b - a)/n
   res := f(a) + f(b)
   lim := n/2

   for i := 1 to lim, do
      oddSum := oddSum + f(a + (2i - 1)h)
   done

   oddSum := oddSum * 4
   for i := 1 to lim-1, do
      evenSum := evenSum + f(a + 2ih)
   done

   evenSum := evenSum * 2
   res := res + oddSum + evenSum
   res := res * (h/3)
   return res
End

উদাহরণ

#include<iostream>
#include<cmath>
using namespace std;

float mathFunc(float x) {
   return (x+(1/x));    //function 1 + 1/x
}

float integrate(float a, float b, int n) {
   float h, res = 0.0, oddSum = 0.0, evenSum = 0.0, lim;
   int i;
   h = (b-a)/n;    //calculate the distance between two interval
   res = (mathFunc(a)+mathFunc(b));    //initial sum using f(a) and f(b)
   lim = n/2;

   for(i = 1; i<=lim; i++)
      oddSum += mathFunc(a+(2*i-1)*h);    //sum of numbers, placed at odd number
   oddSum *= 4;    //odd sum are multiplied by 4

   for(i = 1; i<lim; i++)
      evenSum += mathFunc(a+(2*i)*h);    //sum of numbers, placed at even number
   evenSum *= 2;    //even sum are multiplied by 2
   res += oddSum+evenSum;
   res *= (h/3);
   return res;    //The result of integration
}

main() {
   float result, lowLim, upLim;
   int interval;
   cout << "Enter Lower Limit, Upper Limit and interval: ";
   cin >>lowLim >>upLim >>interval;
   result = integrate(lowLim, upLim, interval);
   cout << "The answer is: " << result;
}

আউটপুট

Enter Lower Limit, Upper Limit and interval: 1 2 20
The answer is: 2.19315