অ-রৈখিক সমীকরণ সমাধানের সেক্যান্ট পদ্ধতি

অ-রৈখিক সমীকরণ সমাধান করতেও সেক্যান্ট পদ্ধতি ব্যবহার করা হয়। এই পদ্ধতিটি নিউটন-র্যাফসন পদ্ধতির অনুরূপ, তবে এখানে আমাদের f(x) ফাংশনের পার্থক্য খুঁজে বের করার দরকার নেই। শুধুমাত্র f(x) ব্যবহার করে, আমরা নিউটনের ডিভাইড ডিফারেন্স সূত্র ব্যবহার করে সংখ্যাগতভাবে f’(x) খুঁজে পেতে পারি। নিউটন-র্যাফসন সূত্র থেকে,

আমরা জানি যে,

এখন, বিভাজন পার্থক্য সূত্র ব্যবহার করে, আমরা পাই,

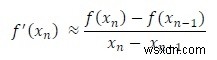
নিউটন-র্যাফসন সূত্রের f’(x) নতুন f’(x) দ্বারা প্রতিস্থাপন করে, আমরা অ-রৈখিক সমীকরণ সমাধানের জন্য সেক্যান্ট সূত্রটি খুঁজে পেতে পারি।

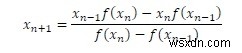
দ্রষ্টব্য: এই পদ্ধতির জন্য, নন-লিনিয়ার সমীকরণের মূল খুঁজে বের করতে আমাদের যেকোনো দুটি প্রাথমিক অনুমান প্রয়োজন।

ইনপুট এবং আউটপুট

Input:
The function f(x) = (x*x) - (4*x) - 10
Output:
The root is: -1.74166

অ্যালগরিদম

secant(x1, x2)

ইনপুট: মূলের জন্য দুটি প্রাথমিক অনুমান।

আউটপুট: একটি নন-লিনিয়ার সমীকরণ f(x) এর আনুমানিক মূল।

Begin
   f1 := f(x1)
   f2 := f(x2)
   x3 := ((f2*x1) – (f1*x2)) / (f2 – f1)
   while relative error of x3 and x2 are > precision, do
      x1 := x2
      f1 := f2
      x2 := x3
      f2 := f(x2)
      x3 := ((f2*x1) – (f1*x2)) / (f2 – f1)
   done
   root := x3
   return root
End

উদাহরণ

#include<iostream>
#include<cmath>
using namespace std;

double absolute(double value) {             //to find magnitude of value
   if(value < 0)
      return (-value);
   return value;
}

double f(double x) {              //the given function x^2-4x-10
   return ((x*x)-(4*x)-10);
}

double secant(double x1, double x2) {
   double x3, root;
   double f1, f2;
   f1 = f(x1);
   f2 = f(x2);
   x3 = (f2*x1-f1*x2)/(f2-f1);

   while(absolute((x3-x2)/x3) > 0.00001) {         //test accuracy of x3
      x1 = x2;           //shift x values
      f1 = f2;
      x2 = x3;
      f2 = f(x2);                 //find new x2
      x3 = (f2*x1-f1*x2)/(f2-f1);          //calculate x3
   }

   root = x3;
   return root;              //root of the equation
}

main() {
   double a, b, res;
   a = 0.5;
   b = 0.75;
   res = secant(a, b);
   cout << "The root is: " << res;
}

আউটপুট

The root is: -1.74166