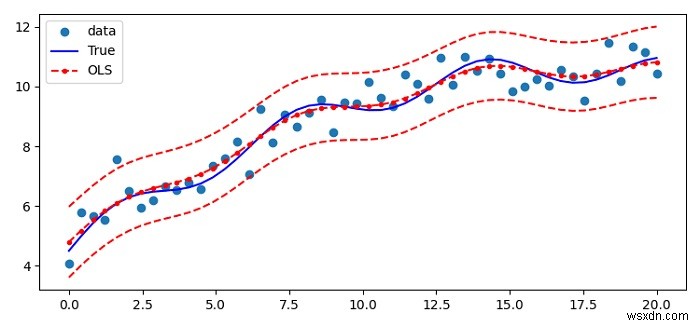
আমরা একটি নন-লিনিয়ার কার্ভের সাথে কিন্তু রৈখিক ডেটা সহ স্ট্যাটসমডেল লিনিয়ার রিগ্রেশন (OLS) প্লট করতে পারি।
পদক্ষেপ
-
চিত্রের আকার সেট করুন এবং সাবপ্লটগুলির মধ্যে এবং চারপাশে প্যাডিং সামঞ্জস্য করুন৷
-
একটি নতুন তৈরি করতে, আমরা seed() ব্যবহার করতে পারি পদ্ধতি।
-
নমুনা এবং সিগমা ভেরিয়েবলের সংখ্যা শুরু করুন।
-
লিনিয়ার ডেটা পয়েন্ট x, X, beta, t_true তৈরি করুন , y এবং res numpy ব্যবহার করে।
-
উত্তর একটি সাধারণ সর্বনিম্ন বর্গ শ্রেণীর উদাহরণ।
-
আদর্শ বিচ্যুতি গণনা করুন। ভবিষ্যদ্বাণীর জন্য আত্মবিশ্বাসের ব্যবধান WLS এবং OLS-এর ক্ষেত্রে প্রযোজ্য, সাধারণ GLS-এর ক্ষেত্রে নয়, অর্থাৎ স্বাধীনভাবে কিন্তু অভিন্নভাবে বিতরণ করা পর্যবেক্ষণ নয়৷
-
সাবপ্লট() ব্যবহার করে একটি চিত্র এবং সাবপ্লটের একটি সেট তৈরি করুন পদ্ধতি।
-
plot() ব্যবহার করে সমস্ত বক্ররেখা প্লট করুন (x, y), (x, y_true), (x, res.fittedvalues), (x, iv_u) সহ পদ্ধতি এবং (x, iv_l) ডেটা পয়েন্ট।
-
প্লটে কিংবদন্তি রাখুন।
-
চিত্রটি প্রদর্শন করতে, শো() ব্যবহার করুন পদ্ধতি।
উদাহরণ
import numpy as np from matplotlib import pyplot as plt from statsmodels import api as sm from statsmodels.sandbox.regression.predstd import wls_prediction_std plt.rcParams["figure.figsize"] = [7.50, 3.50] plt.rcParams["figure.autolayout"] = True np.random.seed(9876789) nsample = 50 sig = 0.5 x = np.linspace(0, 20, nsample) X = np.column_stack((x, np.sin(x), (x - 5) ** 2, np.ones(nsample))) beta = [0.5, 0.5, -0.02, 5.] y_true = np.dot(X, beta) y = y_true + sig * np.random.normal(size=nsample) res = sm.OLS(y, X).fit() prstd, iv_l, iv_u = wls_prediction_std(res) fig, ax = plt.subplots() ax.plot(x, y, 'o', label="data") ax.plot(x, y_true, 'b-', label="True") ax.plot(x, res.fittedvalues, 'r--.', label="OLS") ax.plot(x, iv_u, 'r--') ax.plot(x, iv_l, 'r--') ax.legend(loc='best') plt.show()
আউটপুট