সর্বনিম্ন মানের শীর্ষ থেকে সর্বোচ্চ মানের শীর্ষবিন্দু (পাইথন) এর মধ্যে ন্যূনতম খরচের পথ খুঁজে বের করার জন্য প্রোগ্রাম

ধরুন আমাদের একটি অনির্দেশিত, ওজনযুক্ত গ্রাফ দেওয়া হয়েছে এবং একটি নির্দিষ্ট নোড থেকে অন্য নির্দিষ্ট নোডে ন্যূনতম সম্ভাব্য ভ্রমণ খরচ সহ পথটি খুঁজে বের করতে বলা হয়েছে। ভ্রমণ খরচ নিম্নলিখিত হিসাবে গণনা করা হয়:ধরুন A-> B-> C হিসাবে শীর্ষবিন্দু A থেকে শীর্ষ C এর মধ্যে একটি পথ রয়েছে। A থেকে B পর্যন্ত ভ্রমণের খরচ 10 এবং B থেকে C পর্যন্ত ভ্রমণের খরচ 20 A থেকে C পর্যন্ত ভ্রমণের খরচ হবে (A থেকে B পর্যন্ত ভ্রমণের খরচ) + (B থেকে C থেকে ভ্রমণের খরচের পার্থক্য এবং B নোডে ভ্রমণের ক্রমবর্ধমান খরচ)। সুতরাং এটি 10 + (20 - 10) =20 তে অনুবাদ করবে। আমাদের প্রথম নোড থেকে শেষ নোডের মধ্যে সর্বনিম্ন সম্ভাব্য ভ্রমণের মানগুলি খুঁজে বের করতে হবে (সর্বোচ্চ মান সহ নোডের সর্বনিম্ন মান সহ নোড) একটি প্রদত্ত গ্রাফ।

সুতরাং, যদি ইনপুট মত হয়

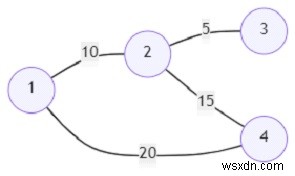
তাহলে আউটপুট হবে 15।

শীর্ষবিন্দু 1 এবং 4 এর মধ্যে দুটি পথ রয়েছে৷ সর্বোত্তম পথটি হল 1->2->4, পথটির মূল্য 10 + (15 - 10) =15৷ অন্যথায়, পথটির দাম 20 হবে৷

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

adjList :=খালি তালিকা সম্বলিত একটি নতুন মানচিত্র
প্রান্তে থাকা প্রতিটি আইটেমের জন্য, করুন
- u :=আইটেম[0]
- v :=আইটেম[1]
- w :=আইটেম[2]
- adjList[u] শেষে জোড়া (w,v) সন্নিবেশ করুন
- adjList[v] এর শেষে জোড়া (w,u) সন্নিবেশ করুন
q :=একটি নতুন গাদা
v_list :=একটি নতুন সেট
q এর শেষে (0,1) সন্নিবেশ করুন
পতাকা :=সত্য
যখন q খালি নয়, কর
- c :=q থেকে সবচেয়ে ছোট আইটেম পপ করুন
- যদি c[1] v_list এ উপস্থিত থাকে, তাহলে
  - পরবর্তী পুনরাবৃত্তির জন্য যান
- v_list এ যোগ করুন(c[1])
- যদি c[1] n এর মত হয়, তাহলে
  - পতাকা :=মিথ্যা
  - রিটার্ন c[0]
- adjList[c[1]]-এ প্রতিটি u-এর জন্য, করুন
  - যদি u[1] v_list এ উপস্থিত না থাকে, তাহলে
    - আউট :=সর্বাধিক (u[0], c[0] ,u[1])
    - পুশ আউট হিপ q এ
যদি পতাকা সত্য হয় তাহলে
- রিটার্ন -1

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

from collections import defaultdict
import heapq
def solve(n, edges):
    adjList = defaultdict(list)
    for item in edges:
        u, v, w = map(int, item)
        adjList[u].append((w,v))
        adjList[v].append((w,u))
    q = []
    v_list = set()
    q.append((0,1))
    flag = True
    while q:
        c = heapq.heappop(q)
        if c[1] in v_list:
            continue
        v_list.add(c[1])
        if c[1] == n:
            flag = False
            return c[0]
        for u in adjList[c[1]]:
            if u[1] not in v_list:
                out = (max(u[0],c[0]),u[1])
                heapq.heappush(q,out)    
    if flag:
        return -1

print(solve(4, [(1, 2, 10), (2, 3, 5), (2, 4, 15), (1, 4, 20)]))

ইনপুট

4, [(1, 2, 10), (2, 3, 5), (2, 4, 15), (1, 4, 20)]