পাইথনের সমস্ত শীর্ষবিন্দুর মধ্যে একটি গ্রাফের মধ্যে ন্যূনতম খরচের যোগফল খুঁজে বের করার প্রোগ্রাম

ধরুন n শীর্ষবিন্দু এবং m প্রান্ত সহ একটি ওজনযুক্ত গ্রাফ রয়েছে। প্রান্তের ওজন 2 এর ক্ষমতায় রয়েছে। গ্রাফের যেকোনো শীর্ষ থেকে যেকোনো শীর্ষে পৌঁছানো যেতে পারে এবং ভ্রমণের খরচ গ্রাফের সমস্ত প্রান্তের ওজনের যোগ করা হবে। আমাদের প্রতিটি জোড়া শীর্ষবিন্দুর মধ্যে ন্যূনতম খরচের যোগফল নির্ধারণ করতে হবে।

সুতরাং, যদি ইনপুট মত হয়

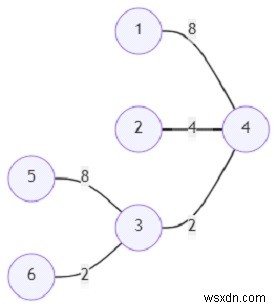
এবং শীর্ষবিন্দুর সংখ্যা (n) =6; তাহলে আউটপুট হবে 2696।

সমস্ত দূরত্বের যোগফল হল 2696।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

একটি ফাংশন par_finder() সংজ্ঞায়িত করুন। এটি i, par
- যদি par[i] -1 এর মত হয়, তাহলে
  - রিটার্ন i
- res :=par_finder(par[i], par)
- পার[i] :=রেস
- রিটার্ন রিটার্ন
একটি ফাংশন সাহায্যকারী() সংজ্ঞায়িত করুন। এর জন্য i, par, w, G, n
- শিশু :=1
- G[i]-এর প্রতিটি আইটেমের জন্য, করুন
  - যদি আইটেম[0] সমান হয়, তাহলে
    - পরবর্তী পুনরাবৃত্তির জন্য যান
  - অন্যথায়,
    - শিশু :=শিশু + সাহায্যকারী(আইটেম[0], আই, আইটেম[1], জি, n)
  - যদি par -1 এর মত না হয়, তাহলে
    - উত্তর :=উত্তর + শিশু * (n - শিশু) *(1 * 2^w)
  - সন্তান ফিরিয়ে দিন
G :=একটি নতুন তালিকা যাতে n + 1টি অন্যান্য তালিকা রয়েছে
কিনারা :=একটি নতুন তালিকা
রাস্তার প্রতিটি আইটেমের জন্য, করুন
- u :=আইটেম[0]
- v :=আইটেম[1]
- w :=আইটেম[2]
- প্রান্তের শেষে সন্নিবেশ করুন (u-1, v-1, w)
প্রান্তের ওজন অনুসারে তালিকার প্রান্তগুলিকে সাজান
par :=n + 1 আকারের একটি নতুন তালিকা -1 দিয়ে শুরু করা হয়েছে
r_edge :=একটি নতুন তালিকা
প্রত্যেক i-এর প্রান্তে, করুন
- যদি par_finder(i[0], par) par_finder(i[1], par) এর মত হয়, তাহলে
  - পরবর্তী পুনরাবৃত্তির জন্য যান
- অন্যথায়,
  - r_edge-এর শেষে i ঢোকান
  - G[i[0]] এর শেষে জোড়া (i[1],i[2]) ঢোকান
  - G[i[1]] এর শেষে জোড়া (i[0],i[2]) ঢোকান
  - par[par_finder(i[0], par)] :=par_finder(i[1], par)
উত্তর :=0
সহায়ক(0, -1, 0, G, n)
উত্তর ফেরত দিন

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def par_finder(i, par) :
    if par[i] == -1 :
         return i
    res = par_finder(par[i], par)
    par[i] = res
    return res

def helper(i, par, w, G, n) :
    global ans
    child = 1
    for item in G[i] :
        if item[0] == par :
            continue
        else :
            child += helper(item[0],i,item[1], G, n)
    if par != -1 :
        ans += child * (n - child) * (1 << w)
    return child

def solve(n, roads):
    global ans
    G = [[] for i in range(n + 1)]
    edges = []
    for item in roads :
        u,v,w = map(int, item)
        edges.append((u-1, v-1, w))
    edges = sorted(edges,key = lambda item : item[2])
    par = [-1 for i in range(n + 1)]
    r_edge = []
    for i in edges :
        if par_finder(i[0], par) == par_finder(i[1], par) :
            continue
        else :
            r_edge.append(i)
            G[i[0]].append((i[1],i[2]))
            G[i[1]].append((i[0],i[2]))
            par[par_finder(i[0], par)] = par_finder(i[1], par)
    ans = 0      
    helper(0, -1, 0, G, n)
    return ans

print(solve(6, [(1,4,8), (2,4,4), (3,4,4), (3,4,2), (5,3,8), (6,3,2)]))

ইনপুট

6, [(1,4,8), (2,4,4), (3,4,4), (3,4,2), (5,3,8), (6,3,2)]