পাইথনে একটি অনির্দেশিত গ্রাফের একটি শীর্ষবিন্দুর কম খরচের পথ আছে কিনা তা খুঁজে বের করার জন্য প্রোগ্রাম

ধরুন, আমাদের একটি ওজনযুক্ত, অনির্দেশিত গ্রাফ দেওয়া হয়েছে। আমাদের একটি ফাংশন কোয়েরি বাস্তবায়ন করতে হবে যা ইনপুট হিসাবে দুটি শীর্ষবিন্দু এবং একটি খরচ 'সীমা' নেয় এবং ইনপুট হিসাবে প্রদত্ত খরচের চেয়ে কম খরচের পথ আছে কিনা তা পরীক্ষা করে। কোনো পথ থাকলে আমরা সত্য ফেরত দিই বা অন্যথায়, আমরা মিথ্যা ফেরত দিই।

সুতরাং, যদি ইনপুট মত হয়

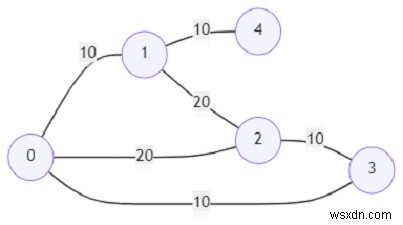
এবং প্রশ্নগুলি হল (0, 2, 10), (3, 1, 30), (4, 3, 30)৷

তাহলে আউটপুট হবে

False
True
True

প্রথম ক্যোয়ারীটির ফলাফলটি মিথ্যা কারণ 10 মূল্যের শীর্ষবিন্দু 0 থেকে 2 এর মধ্যে কোন পথ নেই৷

দ্বিতীয় প্রশ্নের ফলাফল সত্য কারণ মূল্য 10 এর শীর্ষবিন্দু 3 থেকে 1 এর মধ্যে একটি পথ রয়েছে, যা 30 এর কম৷

তৃতীয় প্রশ্নের ফলাফল সত্য কারণ 30 মূল্যের শীর্ষবিন্দু 4 থেকে 3 এর মধ্যে একটি পথ রয়েছে, যা 30 এর সমান৷

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• ওজন :=গ্রাফে বিভিন্ন ওজন ধারণকারী একটি তালিকা

• সংযোগ :=ওজনের জন্য সংযোগ ধারণকারী একটি তালিকা

• ফাংশন query() সংজ্ঞায়িত করুন। এটি p, q, limit

  লাগবে

  • সূচী :=এখানে ওজনের অবস্থান সীমা সাজানো ক্রম বজায় রাখার জন্য বাম দিকে ঢোকানো যেতে পারে

  • যদি সূচক 0 এর মতো হয়, তাহলে

    • রিটার্ন ফলস

  • সংযোগ [index-1, p] সংযোগের মতো হলে সত্য ফেরত দিন[সূচী-1, q]

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

import bisect
class Solution(object):

   def __init__(self, n, edgeList):
      def find(node):
         if parent[node]!=node:
            parent[node] = find(parent[node])
         return parent[node]

      def union(x,y):
         parent[find(y)] = find(x)
         return

      parent = {i:i for i in range(n)}
      edgeList.sort(key = lambda x:x[2])
      self.connections = []
      self.weights = []
      for index,(i,j,weight) in enumerate(edgeList):
         union(i,j)
         if index!=len(edgeList)-1 and weight == edgeList[index+1][2]:
            continue
         self.weights.append(weight)
         self.connections.append([find(i) for i in parent])


   def query(self, p, q, limit):
      index = bisect.bisect_left(self.weights,limit)
      if index==0:
         return False
      return self.connections[index-1][p] == self.connections[index-1][q]

ob = Solution(5, [[0, 1, 10], [0, 2, 20], [1, 4, 10], [0, 3, 10], [1, 2, 20], [2, 3, 10]])
print(ob.query(0, 2, 10))
print(ob.query(3, 1, 30))
print(ob.query(4, 3, 30))

ইনপুট

ob = Solution(5, [[0, 1, 10], [0, 2, 20], [1, 4, 10], [0, 3, 10], [1, 2, 20], [2, 3, 10]])
print(ob.query(0, 2, 10))
print(ob.query(3, 1, 30))
print(ob.query(4, 3, 30))

আউটপুট

False
True
True