পাইথনে একটি প্রদত্ত গ্রাফে বিশেষ ধরনের সাবগ্রাফ খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের কাছে একটি বিশেষ ধরনের গ্রাফ আছে যেটিতে দুই ধরনের শীর্ষবিন্দু রয়েছে যার নাম দেওয়া হয়েছে মাথা এবং পা। গ্রাফটির শুধুমাত্র একটি মাথা রয়েছে এবং সেখানে k প্রান্ত রয়েছে যা মাথাটিকে প্রতিটি পায়ের সাথে সংযুক্ত করে। সুতরাং, যদি আমাদের একটি অনির্দেশিত, ওজনহীন গ্রাফ দেওয়া হয়; আমাদের গ্রাফের শীর্ষবিন্দু বিচ্ছিন্ন সাবগ্রাফগুলিতে এই বিশেষ ধরণের গ্রাফগুলি খুঁজে বের করতে হবে। যেকোন দুটি গ্রাফকে শীর্ষবিন্দু বলা হয় যদি তাদের মধ্যে কোন শীর্ষবিন্দু মিল না থাকে।

সুতরাং, যদি ইনপুট মত হয়

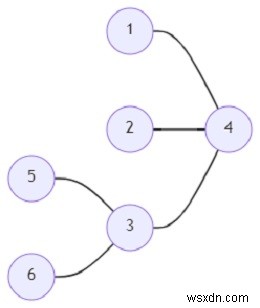
নোডের সংখ্যা (n) =5, ফুটের সংখ্যা (t) =2, তাহলে আউটপুট হবে 5।

এখানে 5টি বিশেষ গ্রাফ থাকতে পারে যা প্রদত্ত গ্রাফের শীর্ষবিন্দু বিচ্ছিন্ন সাবগ্রাফ।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

G :=একটি নতুন তালিকা যাতে n+1 খালি তালিকা রয়েছে
প্রান্তে থাকা প্রতিটি আইটেমের জন্য, করুন
- s :=আইটেম[0]
- d :=আইটেম[1]
- G[s] এর শেষে d ঢোকান
- G[d] এর শেষে s ঢোকান
ভিজিট করুন :=একটি নতুন মানচিত্র
আমি 0 থেকে n রেঞ্জের জন্য, কর
- v :=G[i]
- যদি v এর আকার 1 এর মতো হয়, তাহলে
  - s :=v[0]
  - যদি ভিজিটে উপস্থিত না থাকে, তাহলে
    - ভিজিট[গুলি] :=[i]
  - অন্যথায়,
    - পরিদর্শন[গুলি] শেষে i যোগ করুন
- অন্যথায় যখন v এর আকার 0 এর মত হয়, তখন
  - n :=n - 1
tmp :=0
ভিজিটের প্রতিটি k-এর জন্য, করুন
- x :=পরিদর্শনের আকার[k] -t
- যদি x> 0, তারপর
  - tmp :=tmp + x
রিটার্ন n - tmp

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def solve(n, t, edges):
    G = [[] for _ in range(n + 1)]
    for item in edges:
        s, d = map(int, item)
        G[s].append(d)
        G[d].append(s)
    visit = {}
    for i in range(n):
        v = G[i]
        if len(v) == 1:
            s = v[0]
            if s not in visit:
                visit[s] = [i]
            else: visit[s].append(i)
        elif len(v) == 0:
            n -= 1
    tmp = 0
    for k in visit:
        x = len(visit[k])-t
        if x > 0:
            tmp += x
    return n - tmp

print(solve(6, 2, [(1,4), (2,4), (3,4), (3,4), (5,3), (6,3)]))

ইনপুট

6, 2, [(1,4), (2,4), (3,4), (3,4), (5,3), (6,3)]