একটি গ্রাফের বৃহত্তম চক্রের সর্বনিম্ন আকার খুঁজে বের করার জন্য প্রোগ্রাম (পাইথন)

ধরুন আমাদের একটি গ্রাফ দেওয়া হয়েছে এবং গ্রাফের বৃহত্তম চক্রের সর্বনিম্ন আকার খুঁজে বের করতে বলা হয়েছে। একটি গ্রাফের একটি চক্র হল একটি গ্রাফের একটি উপসেট যেখানে প্রতিটি জোড়া শীর্ষবিন্দু সংলগ্ন থাকে, অর্থাৎ প্রতিটি জোড়া শীর্ষবিন্দুর মধ্যে একটি প্রান্ত থাকে। একটি গ্রাফে বৃহত্তম চক্রটি খুঁজে পাওয়া বহুপদী সময়ে সম্ভব নয়, তাই একটি ছোট গ্রাফের নোড এবং প্রান্তের সংখ্যা বিবেচনা করে আমাদের এটির বৃহত্তম চক্রটি খুঁজে বের করতে হবে৷

সুতরাং, যদি ইনপুট নোডের মত হয় =4, প্রান্ত =4; তাহলে আউটপুট হবে 2।

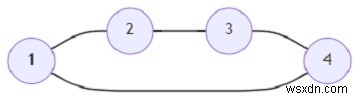
উপরের গ্রাফে, একটি চক্রের সর্বোচ্চ আকার হল 2।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• একটি ফাংশন সাহায্যকারী() সংজ্ঞায়িত করুন। এটি x, y
  লাগবে
  • ga :=x mod y
  • gb :=y - ga
  • sa :=(x / y) + 1 এর মানের ভাগফল
  • sb :=(x / y) এর মানের ভাগফল
  • রিটার্ন ga * gb * sa * sb + ga * (ga - 1) * sa * sa / 2 + gb * (gb - 1) * sb * sb / 2
• i :=1
• j :=নোড + 1
• যখন i + 1
• p :=i + ফ্লোর মান ((j - i) / 2)
• k :=সাহায্যকারী(নোড, পি)
• যদি k <প্রান্ত হয়, তাহলে
  • i :=p
• অন্যথায়,
  • j :=p

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

import math
def helper(x, y):
    ga = x % y
    gb = y - ga
    sa = x // y + 1
    sb = x // y
    return ga * gb * sa * sb + ga * (ga - 1) * sa * sa // 2 + gb * (gb - 1) * sb * sb // 2

def solve(nodes, edges):
    i = 1
    j = nodes + 1
    while i + 1 < j:
        p = i + (j - i) // 2
        k = helper(nodes, p)
        if k < edges:
            i = p
        else:
            j = p
    return j

print(solve(4, 4))

ইনপুট

4,4

আউটপুট

2