পাইথনে সাব-ট্রির নোড মানের সমষ্টি থেকে ন্যূনতম মান বের করার প্রোগ্রাম

ধরুন, আমাদের একটি গাছ আছে যার সমস্ত নোড সংখ্যা 1 থেকে n পর্যন্ত। প্রতিটি নোডের একটি পূর্ণসংখ্যা মান রয়েছে। এখন যদি আমরা গাছ থেকে একটি প্রান্ত অপসারণ করি, তাহলে দুটি সাব-ট্রির নোডের মানের যোগফলের পার্থক্য ন্যূনতম হতে হবে। আমাদের এই জাতীয় উপ-বৃক্ষের মধ্যে ন্যূনতম পার্থক্য খুঁজে বের করতে হবে এবং ফেরত দিতে হবে। গাছটি আমাদেরকে প্রান্তের সংগ্রহ হিসাবে দেওয়া হয় এবং নোডের মানও দেওয়া হয়।

সুতরাং, যদি ইনপুটটি হয় n =6, edge_list =[[1, 2], [1, 3], [2, 4], [3, 5], [3, 6]], মান =[15, 25, 15, 55, 15, 65], তাহলে আউটপুট হবে 0।

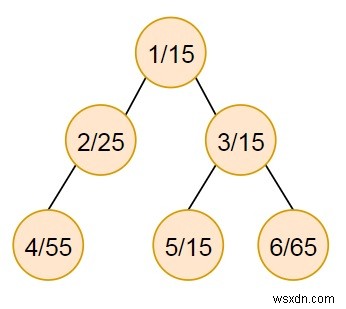
যদি প্রান্ত (1,2) সরানো হয়, তাহলে ওজনের যোগফল 80, 110 হবে। পার্থক্য হল 30।

যদি প্রান্ত (1,3) সরানো হয়, তাহলে ওজনের যোগফল 95, 95 হবে। পার্থক্য হল 0।

যদি প্রান্ত (2,4) সরানো হয়, তাহলে ওজনের যোগফল 55, 135 হবে। পার্থক্য হল 80।

যদি প্রান্ত (3,5) সরানো হয়, তাহলে ওজনের যোগফল 15, 175 হবে। পার্থক্য হল 160।

যদি প্রান্ত (3,6) সরানো হয়, তাহলে ওজনের যোগফল 65, 125 হবে। পার্থক্য হল 60।

তাই সর্বনিম্ন ওজন হল 0।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

adj_list :=আকার n এর একটি নতুন তালিকা যেখানে খালি তালিকা রয়েছে
এজ_লিস্টের প্রতিটি প্রান্তের জন্য, করুন
- u :=প্রান্ত[0]
- v :=প্রান্ত[1]
- adj_list[u-1] এর শেষে v-1 ঢোকান
- adj_list[v-1] এর শেষে u-1 ঢোকান
value_list :=0s দিয়ে শুরু করা n আকারের একটি নতুন তালিকা
not_visited :=i আকারের একটি নতুন মানচিত্র, যেখানে i হল adj_list এ খালি না থাকা তালিকার সংখ্যা
যদিও not_visited খালি নয়, করুন
- প্রত্যেকটি i in not_visited, do
  - value_list[i] :=value_list[i] + values[i]
  - যদি (adj_list[i]) এর দৈর্ঘ্য অ-শূন্য হয়, তাহলে
    - adj_list[adj_list[i, 0]] থেকে i মুছুন
    - value_list[adj_list[i, 0]] :=value_list[adj_list[i, 0]] + value_list[i]
- প্রত্যেকটি i in not_visited, do
  - যদি len(adj_list[i]) এবং len(adj_list[adj_list[i, 0]]) ==1, তারপর
    - not_visited :=adj_list[i, 0] ধারণকারী একটি নতুন তালিকা
return_val :=|sum(values) - 2 * value_list[0]|
1 থেকে n রেঞ্জের জন্য, করুন
- decision_val :=|sum(values) - 2 * value_list[i]|
- যদি সিদ্ধান্ত_ভাল
- রিটার্ন_ভাল :=সিদ্ধান্ত_ভাল

রিটার্ন রিটার্ন_ভাল

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

def solve(n, edge_list, values):adj_list =[[] i for range(n)] edge_list এ প্রান্তের জন্য:u =edge[0] v =edge[1] adj_list[u-1]। যোগ করুন (len(not_visited)):for i in not_visited:value_list[i] +=values[i] if(len(adj_list[i])):adj_list[adj_list[i][0]].remove(i) value_list[ adj_list[i][0]] +=value_list[i] not_visited ={adj_list[i][0] এর জন্য i in not_visited যদি len(adj_list[i]) এবং len(adj_list[adj_list[i][0]]) ==1} return_val =abs(sum(values) - 2 * value_list[0]) in range(1, n):ডিসিশন_ভাল =abs(সমষ্টি(মান) - 2 * মান_তালিকা[i]) যদি ডিসিশন_ভাল  ইনপুট
 <প্রে>6, [[1, 2], [1, 3], [2, 4], [3, 5], [3, 6]], [10, 20, 10, 50, 10, 60]