নেতিবাচক পূর্ণসংখ্যার সাথে মাইক্রোপ্রসেসর রোম্যান্স - সিপিইউ পাটিগণিত ডিজাইনের কীভাবে এবং কেন

কম্পিউটার সম্পর্কে আমরা প্রথম যা শিখি তার মধ্যে একটি হল তারা শুধুমাত্র 0 এবং 1s বোঝে , অথবাবিট .

আমরা মানুষ, অন্যদিকে, দশমিক পদ্ধতির মাধ্যমে সংখ্যার সাথে যোগাযোগ করি। এই সিস্টেম ধনাত্মক বা ঋণাত্মক সংখ্যা বোঝাতে প্লাস এবং বিয়োগ চিহ্ন (+ এবং -) সহ 0 থেকে 9 পর্যন্ত সংখ্যা ব্যবহার করে।

যেহেতু কম্পিউটার শুধুমাত্র দুটি সংখ্যা ব্যবহার করতে পারে – 0 এবং 1 - আগের দিনের প্রকৌশলী এবং গণিতবিদরা নেতিবাচক সংখ্যাগুলিকে উপস্থাপন করার জন্য এবং তাদের সাথে পাটিগণিত করার জন্য চতুর কৌশলগুলি ডিজাইন করেছিলেন। আসুন সেই কৌশলগুলির সৌন্দর্য অন্বেষণ করি।

প্রথম, কম্পিউটার কীভাবে কাজ করে তার কিছু পটভূমি

সফ্টওয়্যার, ছবি, টেক্সট, ভিডিও, সংখ্যা এবং এর মধ্যে থাকা সবকিছুই আমাদের কম্পিউটারের সর্বনিম্ন স্তরে 0 এবং 1 সেকেন্ড।

ইমেজ, টেক্সট, ভিডিও এবং সংখ্যার জন্য, আমাদের এনকোডিং স্কিম আছে যেগুলো স্থির করে যে এই জিনিসগুলি কীভাবে 0 এবং 1 সেকেন্ডে যাবে। উদাহরণস্বরূপ, পাঠ্যের জন্য ASCII এবং ইউনিকোড।

আমরা যে সফ্টওয়্যার প্রোগ্রামগুলি কোড করি সেগুলি কম্পাইলার এবং অ্যাসেম্বলারের মাধ্যমে 0s এবং 1s এ পাই। 0s এবং 1s-এর যে সেটগুলি মেশিন কোড (বা মেশিন নির্দেশনা) নামে পরিচিত তা প্রসেসর চালানোর আগে প্রথমে আমাদের কম্পিউটারের প্রধান মেমরিতে (RAM) সংরক্ষণ করা হয়।

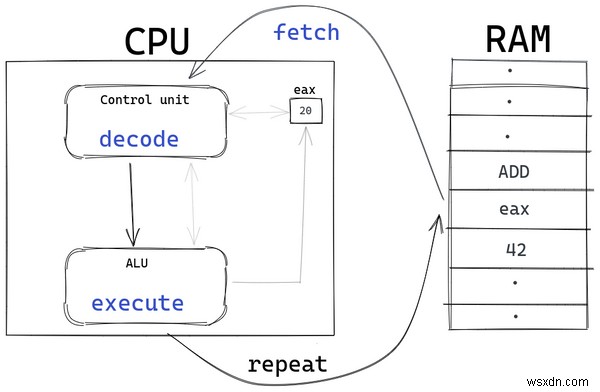
প্রসেসর আনয়ন করে এক্সিকিউশন চক্র শুরু করে প্রধান মেমরি থেকে নির্দেশাবলী, তারপর প্রসেসরের নিয়ন্ত্রণ ইউনিট ডিকোড এই নির্দেশাবলী দুটি ভাগে বিভক্ত - অপারেশন কোড (অপকোড) এবং অপারেন্ড।

অপকোড পরবর্তী পদক্ষেপের সিদ্ধান্ত নেয় যা সম্পাদন করতে হবে যেমন ADD (সংযোজন), JMP (জাম্প), INC (বৃদ্ধি) ইত্যাদি। অপারেন্ডগুলি হল সেই মানগুলি (বা মেমরির অবস্থানগুলি) যার উপর সেই অপারেশনটি করা হবে৷

ডিকোড করা নির্দেশাবলী এক্সিকিউশনের জন্য পাটিগণিত ও লজিক ইউনিটে (ALU) পাঠানো হয় . ALU-তে, নির্দেশটি অপারেন্ডের অপকোডের উপর ভিত্তি করে কার্যকর করা হয় এবং ফলাফল মেমরিতে সংরক্ষিত হয়।

উদাহরণস্বরূপ, সমাবেশ কোড ADD eax, 42 অ্যাসেম্বলার দ্বারা প্রথমে মেশিন কোডে (0s এবং 1s) পরিণত হয়। তারপর ফেচ-ডিকোড-এক্সিকিউট চক্র শুরু হওয়ার আগে এটি প্রধান মেমরিতে সংরক্ষণ করা হয়।

যখন ADD eax, 42 এর জন্য মেশিন কোড আনা হয় মেমরি শেষ থেকে, নির্দেশনা ডিকোড করা হয়। ডিকোড করা আউটপুট বলে যে opcode হল ADD এবং অপারেন্ডগুলি হল eax এবং 42 .

eax একটি রেজিস্টার - প্রসেসরের মধ্যে অন্তর্নির্মিত একটি মেমরি অবস্থান যা প্রসেসর দ্বারা তাত্ক্ষণিকভাবে অ্যাক্সেস করা যায়। eax বেশিরভাগ প্রসেসরে রেজিস্টারকে একুমুলেটর বলা হয়।

ADD eax, 42 সমাবেশ কোডটি eax এর বর্তমান মানের সাথে 42 যোগ করার জন্য ডিজাইন করা হয়েছে নিবন্ধন করুন (সংগ্রহকারী) এবং সঞ্চয় করুন যে যোগফল eax . এটি হল eax = eax + 42 .

ধরুন যে বর্তমানে eax হল 20। এর মানে হল eax এর মান ADD eax, 42 চালানোর পরে হবে 20 + 42 =62।

EDVAC-এর মতো প্রাথমিক কম্পিউটারগুলির নকশা ক্লান্তিকর গাণিতিক গণনাগুলিকে সহজ এবং দ্রুত করার ইচ্ছা নিয়ে শুরু হয়েছিল।

কম্পিউটার কম্পিউট তৈরির সম্পূর্ণ দায়িত্ব অ্যাডারদের কাঁধে - সার্কিট যা দুটি সংখ্যা যোগ করে। কারণ বিয়োগ, গুণ এবং ভাগের মতো অত্যাধুনিক ক্রিয়াকলাপগুলি তাদের সার্কিটে যোগকারীকে ব্যবহার করে।

শেষ পর্যন্ত কম্পিউটারগুলি যুক্তির ক্ষমতা সহ একটি দ্রুত গাণিতিক মেশিন। বাইনারি গাণিতিক ডিজাইনের (ধনাত্মক এবং বিশেষ করে নেতিবাচক পূর্ণসংখ্যার) চ্যালেঞ্জগুলি এবং সৌন্দর্য বোঝা হল একটি কম্পিউটার প্রসেসরের সবচেয়ে মৌলিক ধারণাগুলির মধ্যে একটি .

আসুন প্রথমে দেখি কিভাবে দশমিক সংখ্যা বাইনারিতে উপস্থাপন করা হয় এবং কিভাবে দুটি বাইনারি মান যোগ করা যায়। তারপর আমরা সৌন্দর্য অন্বেষণ শুরু হবে.

বাইনারি সিস্টেম কিভাবে কাজ করে

আমি যদি আপনাকে 872500 পড়তে বলি , আপনি সম্ভবত বলবেন 872.5K . আসুন আমাদের মন কীভাবে এটি করে তা দেখে নেওয়া যাক।

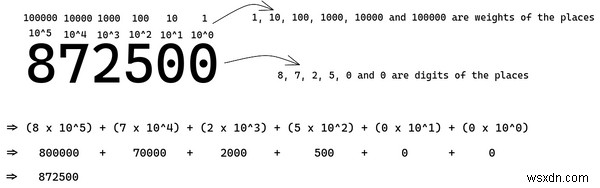
আমরা ডান দিক থেকে প্রথম অঙ্কে একজনের স্থান নির্ধারণ করি, তারপর ডান থেকে দ্বিতীয়টিতে দশের স্থান, শতভাগ থেকে তৃতীয়, এবং আরও অনেক কিছু, প্রতিবার 10 এর শক্তি দ্বারা বৃদ্ধি পাই৷

প্রতিটি স্থানে 10 এর এই শক্তিগুলি স্থানগুলির ওজন। শততম স্থানের ওজন একশত। আমরা প্রতিটি স্থানের সংখ্যাগুলিকে তাদের স্থানের ওজন দ্বারা গুণ করি এবং একটি সম্পূর্ণ সংখ্যা পেতে সেগুলিকে যোগ করি।

উপরের ডায়াগ্রামে, আপনি দেখতে পাচ্ছেন যে প্রতিটি স্থানের ওজনের বৃদ্ধি 10 এর শক্তিতে, 10^0 থেকে শুরু করে এবং 10^5 দিয়ে যাচ্ছে . এজন্য দশমিককে বেস টেন সিস্টেম বলা হয়।

বাইনারিতে, প্রতিটি স্থানের ওজন 2 শক্তি দ্বারা বৃদ্ধি পায়। এর মানে হল যে স্থানের ওজন 2^0 থেকে শুরু হয় এবং 2^something এ শেষ হয় . এটাই একমাত্র পার্থক্য।

00110101 দশমিকে 53-এ অনুবাদ করা হয়। কম্পিউটারগুলি বাইনারিকে একইভাবে ব্যাখ্যা করে যেভাবে আমরা মানুষ দশমিককে ব্যাখ্যা করি, যা প্রতিটি স্থানের অঙ্ককে তার ওজন দ্বারা গুণ করে এবং তাদের সংক্ষিপ্ত করে।

কিভাবে 1s এবং 0s যোগ করবেন

সংযোজন বাইনারিতে প্রায় একইভাবে কাজ করে যেমন এটি দশমিকে করা হয়। একটি উদাহরণের মাধ্যমে তা দেখা যাক। আমরা দুটি বাইনারি সংখ্যা যোগ করব:1101 (13) এবং 1100 (12)।

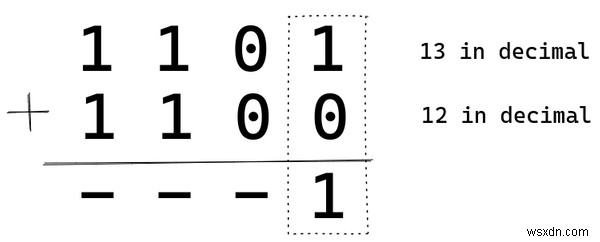
আমরা যেমন দশমিক পদ্ধতিতে করি, আমরা একজনের স্থান থেকে শুরু করি (2^0 ) 1 এবং 0 যোগ করলে আমাদের 1 পাওয়া যায়। তাই আমরা সেখানে 1 রাখি। আমার সাথে থাকুন এবং আপনি পুরো ছবি পাবেন।

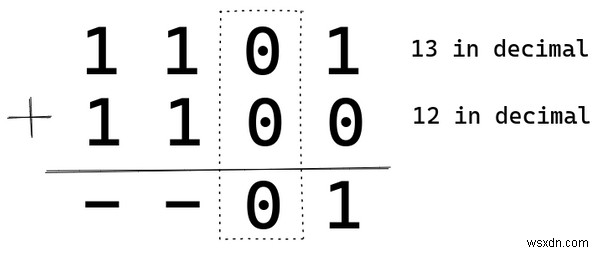
0 যোগ 0 হল 0। এগিয়ে চলছি।

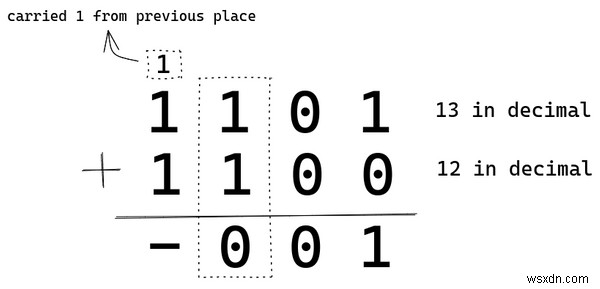
1 যোগ 1 হল 2। এবং 2 কে বাইনারিতে 10 হিসাবে উপস্থাপন করা হয় . আমরা 1কে পরের স্থানে নিয়ে যাই এবং বর্তমান যে স্থানে আছি তার ফলস্বরূপ 0 রাখি। এটি কি দশমিক যোগে একটি স্থানে 9 অতিক্রম করার সমান নয়?

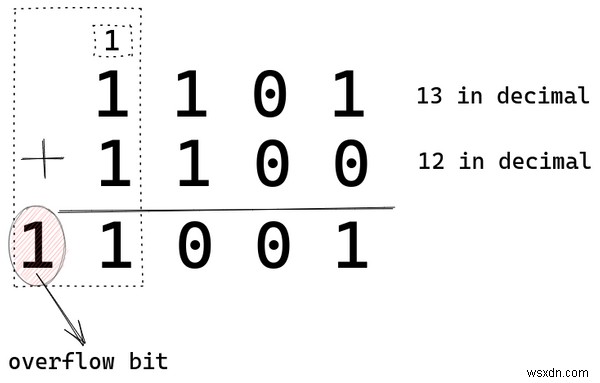
আমাদের সেখানে দুটি 1s এবং একটি 1 যা পূর্ববর্তী স্থান থেকে এগিয়ে নেওয়া হয়েছিল, তাই মোট তিনটি 1s আছে। তাদের যোগফল হবে 3, এবং বাইনারি 3-এ 11 তাই আমরা 11 লিখি . চূড়ান্ত ফলাফল হল 11001 অথবা 25 দশমিক আকারে, যা প্রকৃতপক্ষে 13 + 12।

উপরের গণনাটি অনুমান করে যে ফলাফল সংরক্ষণ করার জন্য আমাদের কাছে পাঁচটি বিট উপলব্ধ রয়েছে। যদি একটি 4-বিট কম্পিউটার এই সংযোজন করে, তবে ফলাফল সংরক্ষণ করার জন্য এটিতে কেবলমাত্র চারটি বিট উপলব্ধ থাকবে।

সেই পঞ্চম বিটটিকে একটি ওভারফ্লো বলা হবে৷ 4-বিট কম্পিউটারে। পূর্ণসংখ্যার পাটিগণিতের মধ্যে, ওভারফ্লো বিট উপেক্ষা করা হয় বা বাতিল করা হয়। তাই আমরা পেতাম 1001 (9) আমাদের ফলাফল হিসাবে যদি আমরা একটি 4-বিট কম্পিউটার ব্যবহার করি।

বাইনারী গাণিতিক নকশার সৌন্দর্য

আমরা এগিয়ে যাওয়ার আগে দুটি গুরুত্বপূর্ণ পদ আমাদের বুঝতে হবে তা হল অন্যতম তাৎপর্যপূর্ণ বিট এবং সবচেয়ে উল্লেখযোগ্য বিট .

ডানদিকের বিটটি সবচেয়ে কম উল্লেখযোগ্য বিট কারণ এটির স্থানের ওজন সবচেয়ে ছোট (2^0 ) এবং বামদিকের বিটটি সবচেয়ে উল্লেখযোগ্য বিট যেহেতু এটির সর্বোচ্চ স্থানের ওজন রয়েছে (2^7 )।

যদি বিশ্বের শুধুমাত্র ধনাত্মক সংখ্যা থাকত, তাহলে এই নিবন্ধের শেষ হবে (কারণ আমরা ইতিমধ্যে শিখেছি কিভাবে বাইনারিতে দশমিককে উপস্থাপন করতে হয় এবং কীভাবে বাইনারিতে যোগ করতে হয়)।

সৌভাগ্যক্রমে, আমাদেরও নেতিবাচক সংখ্যা রয়েছে।

সিপিইউ এর গাণিতিক নকশার সৌন্দর্য নেতিবাচকতায় রয়ে গেছে।

তাহলে কম্পিউটার কিভাবে ঋণাত্মক সংখ্যার প্রতিনিধিত্ব করে এবং কিভাবে ঋণাত্মক সংখ্যার উপর পাটিগণিত কাজ করে? আসুন এই সমস্যার একটি এনকোডিং পদ্ধতি দেখি।

অনুগ্রহ করে মনে রাখবেন যে নীচের বিভাগগুলিতে আমরা ধারণাগুলি বোঝার জন্য একটি 4-বিট কম্পিউটারের সাথে কাজ করব, যার অর্থ পঞ্চম বিটটিকে একটি ওভারফ্লো হিসাবে বিবেচনা করা হবে। গাণিতিক করতে 16-বিট, 32-বিট বা 64-বিটের মতো সমস্ত CPU আর্কিটেকচারে একই নীতি প্রযোজ্য।

সাইন ম্যাগনিটিউড এনকোডিং পদ্ধতি

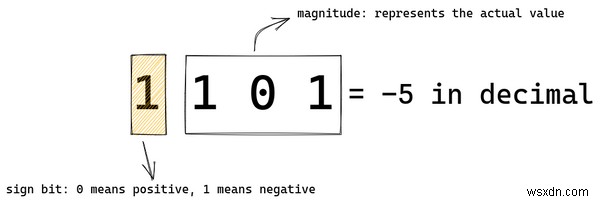
1101 এই এনকোডিং স্কিমে দশমিক আকারে -5 হবে। সবচেয়ে বাম বা সবচেয়ে উল্লেখযোগ্য বিট হল সাইন বিট। এটি সংখ্যার চিহ্ন সম্পর্কে প্রসেসরকে বলে – অর্থাৎ সংখ্যাটি ধনাত্মক বা ঋণাত্মক কিনা।

0 সাইন বিটে একটি ইতিবাচক মান এবং 1 প্রতিনিধিত্ব করে একটি নেতিবাচক মান প্রতিনিধিত্ব করে। অবশিষ্ট বিট আমাদের প্রকৃত মাত্রা বলে।

1101-এ , সাইন বিট হল 1 তাই সংখ্যাটি ঋণাত্মক। 101 দশমিকে 5 সমান। তাই 1101 দশমিকে -5 গণনা করা হবে।

উপরের চিত্রটিতে আপনি সমস্ত পূর্ণসংখ্যা দেখতে পাবেন যা এই এনকোডিং পদ্ধতি ব্যবহার করে চারটি বিট দ্বারা প্রতিনিধিত্ব করা যেতে পারে। এই বিন্দু পর্যন্ত সব ভাল দেখায়.

কিন্তু যদি আমরা ঘনিষ্ঠভাবে তাকাই, আমরা এই এনকোডিং স্কিমে একটি খুব গুরুতর ডিজাইন সমস্যা দেখতে পাব। আসুন সেই সমস্যার মুখোমুখি হই।

আসুন একটি ধনাত্মক এবং একটি ঋণাত্মক সংখ্যা যোগ করি। উদাহরণস্বরূপ আমরা +4 এবং -1 যোগ করব। আমাদের উত্তর (+4) + (-1) = (+3) হওয়া উচিত সেটি হল 0011 .

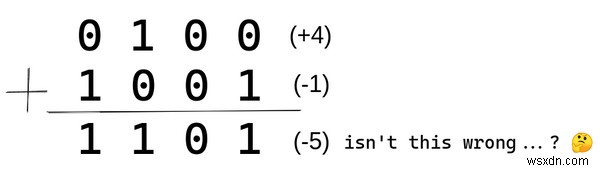
দেখুন, ফলাফল হল 1101 (-5)। প্রকৃত উত্তর 0011 হওয়া উচিত (+3)। যদি আমরা একটি প্রসেসরে এই পদ্ধতির প্রয়োগ করি তবে এই সমস্যাটি মোকাবেলা করার জন্য আমাদের যুক্তি যোগ করতে হবে এবং ইঞ্জিনিয়াররা তাদের যুক্তিতে অতিরিক্ত জটিলতা ঘৃণা করে।

আমরা আরো সার্কিট যোগ করার সাথে সাথে, শক্তি খরচ বৃদ্ধি পায় এবং কর্মক্ষমতা ক্ষতিগ্রস্ত হয়।

আধুনিক ট্রানজিস্টর-ভিত্তিক কম্পিউটারগুলির জন্য এটি একটি তুচ্ছ সমস্যা বলে মনে হতে পারে।

কিন্তু EDVAC-এর মতো প্রথম দিকের কম্পিউটারের কথা চিন্তা করুন যা হাজার হাজার ভ্যাকুয়াম টিউবে চালিত হয় যা দিনে শত শত লোক দ্বারা চালিত কিলোওয়াট শক্তি ব্যবহার করে। আর এগুলো তৈরি করতে সরকার খরচ করেছে লাখ লাখ টাকা।

সেই দিনগুলিতে অতিরিক্ত সার্কিট এবং ভ্যাকুয়াম টিউব স্থাপনের অর্থ ছিল হাজার হাজার ডলার এবং রক্ষণাবেক্ষণের গুরুতর সমস্যা।

তাই ইঞ্জিনিয়ারদের একটি স্মার্ট এনকোডিং ডিজাইনের কথা ভাবতে হয়েছিল।

এখন, সময় এসেছে সেই সৌন্দর্য প্রকাশ করার যা এই সমস্যাটি মোকাবেলা করবে এবং আমাদের সিস্টেমকে আরও সহজ, আরও কর্মক্ষম এবং কম শক্তির ক্ষুধার্ত করে তুলবে৷

একটি সুন্দর এনকোডিং সিস্টেম প্রবেশ করে এবং CPU জ্বলজ্বল করে ❤️

এই এনকোডিং স্কিমটিতে, আগেরটির মতো, বামদিকের বিটটি একটি সাইন বিট হিসাবে কাজ করে - তবে নেতিবাচক সংখ্যাগুলিকে উপস্থাপন করার জন্য কিছু শিল্প জড়িত৷

ধনাত্মক সংখ্যাগুলি পূর্ববর্তী এনকোডিং স্কিমের মতো ঠিক একইভাবে উপস্থাপন করা হয়:একটি অগ্রণী 0 এর পরে মাত্রার জন্য অবশিষ্ট বিট। উদাহরণস্বরূপ, এই এনকোডিং স্কিমেও, 6 কে 0110 হিসাবে উপস্থাপন করা হবে .

একটি ঋণাত্মক সংখ্যার প্রতিনিধিত্ব করার জন্য, একটি দুই ধাপের গণিত প্রক্রিয়াটি তার ধনাত্মক অংশে চালানো হয়। -6 এর প্রতিনিধিত্ব করার অর্থ হল আমরা বাইনারিতে -6 পেতে +6 তে একটি দুই ধাপের গণিত প্রক্রিয়া করব।

আসুন দেখি কিভাবে -6 বাইনারিতে এনকোড করবে:

পূর্ববর্তী সাইন ম্যাগনিটিউড পদ্ধতিতে, +6 এর নেতিবাচক গণনা করার জন্য, আমরা কেবল 0 থেকে সাইন বিট পরিবর্তন করতাম। 1 এ . 0110 (+6) হয়ে যাবে 1110 (-6)।

এই নতুন এনকোডিং স্কিমে, আমরা প্রথমে বিটগুলিকে উল্টে দিই। শূন্য থেকে এক এবং এককে শূন্যে পরিবর্তন করা হচ্ছে। 0110 (+6) 1001 হয়ে যায় . বিটগুলিকে উল্টানোকে "একজনের পরিপূরক" বলা হয়, তাই এখানে আমরা 0110 এর পরিপূরক গণনা করেছি। ফলে 1001 . তারপর...

আমরা 0001 যোগ করি (+1) একজনের পরিপূরক আমরা প্রথম ধাপ থেকে পেয়েছি (1001 ) ফলাফল 1010 -6 এর বাইনারি উপস্থাপনা হবে। এই এনকোডিং স্কিমটিকে দুইয়ের পরিপূরক বলা হয়। তাই মনে রাখবেন যে একটি ধনাত্মক পূর্ণসংখ্যার দুটির পরিপূরক গণনা করা আমাদের এর নেতিবাচক প্রতিরূপ দেয়৷

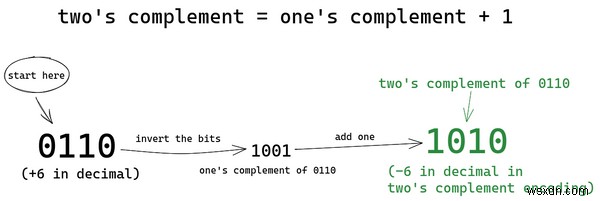
ইনভার্টিং বিট আমাদের একের পরিপূরক দেয়। একটির পরিপূরকের সাথে একটি যোগ করলে আমাদের দুটি মূল বিটের পরিপূরক হয় যা দিয়ে আমরা শুরু করেছি। সহজ, তাই না?

এখন, দেখা যাক কেন এই এনকোডিং স্কিমটি এত সুন্দর। আমরা 0100 যোগ করব (+4) এবং 1111 (-1)।

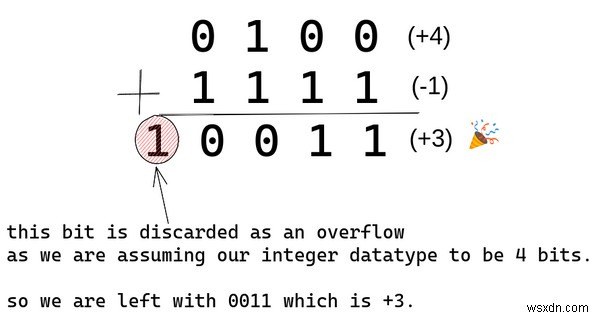
দেখুন, আমরা দুটির পরিপূরক এনকোডিং স্কিম দিয়ে সঠিক ফলাফল পাই। এখন আমরা তাদের চিহ্ন সম্পর্কে চিন্তা না করে পূর্ণসংখ্যা যোগ করতে পারি।

আমরা শিখেছি কিভাবে একটি ঋণাত্মক পূর্ণসংখ্যা 0s এবং 1s-এ দুইটির পরিপূরক এনকোডিংয়ের মাধ্যমে উপস্থাপন করা যায়। এখন ধরুন আমরা ADD eax, -3 এক্সিকিউট করি এবং eax রেজিস্টারে বর্তমান মান হল -1। সুতরাং ADD eax, -3 কার্যকর করার পরে eax-এ মান হবে -4 (যা 1100 দুই এর পরিপূরক এনকোডিং)।

যখন অপারেটিং সিস্টেম 1100 পুনরুদ্ধার করে eax থেকে ব্যবহারকারীর কাছে ফলাফল উপস্থাপন করতে, অপারেটিং সিস্টেম কিভাবে 1100 ডিকোড করে দশমিক থেকে? অথবা ধরুন আমরা যদি একজন প্রোগ্রামার হিসেবে 1100 জুড়ে আসি , কিভাবে আমরা 1100 সংখ্যাটি বের করতে পারি প্রতিনিধিত্ব করে?

আমরা কখন 1100 হিট করি তা দেখার জন্য অবশ্যই আমরা প্রতিটি ধনাত্মক পূর্ণসংখ্যার দুটি পরিপূরক গণনা চালিয়ে যেতে পারি না . যে খুব ধীর হবে.

প্রোগ্রামার এবং ওএস বাইনারিকে দশমিকে ডিকোড করতে দুইয়ের পরিপূরকের একটি সুন্দর বৈশিষ্ট্য ব্যবহার করে।

যখন আমরা একটি ধনাত্মক সংখ্যার দুটির পরিপূরক গণনা করি, তখন আমরা এর ঋণাত্মক প্রতিরূপ পাই। আচ্ছা, বিপরীতটাও সত্য - যার অর্থ একটি ঋণাত্মক সংখ্যার দুটির পরিপূরক গণনা করা আমাদেরকে এর ধনাত্মক প্রতিরূপ দেবে। আমরা এক মিনিটের মধ্যে এটি কেন দেখতে হবে.

প্রথমে, আসুন বুঝতে পারি কিভাবে OS বা একটি প্রোগ্রামার 1100 ডিকোড করবে দশমিক থেকে।

1100 পুনরুদ্ধার করার সময় eax রেজিস্টার থেকে, OS 1 দেখে সাইন বিট হিসাবে যা সংকেত দেয় যে পূর্ণসংখ্যা নেতিবাচক। 1100 এর দুই পরিপূরক গণনা করা হয় যা 1100 এর ধনাত্মক প্রতিরূপ দেয় যা 0100 হিসাবে বেরিয়ে আসে (+4)। OS তারপর ইতিবাচক প্রতিরূপের উপর একটি নেতিবাচক চিহ্ন প্রিপেন করে এবং চূড়ান্ত উত্তরটি -4 হিসাবে প্রদান করে। এই অনুচ্ছেদটি আবার পড়ুন এবং আপনি আরও ভালভাবে বুঝতে পারবেন।

তারপর সিপিইউ হেসে বিদায় জানালো আজকের জন্য;)

সিপিইউ তার মায়ের সাথে দেখা করতে তার বাড়িতে গেছে। দুজনের পরিপূরক শিল্পের অভ্যন্তরীণ কাজগুলি নিয়ে আলোচনা করার জন্য এখন আমাদের কাছে প্রচুর সময় আছে৷

দুজনের পরিপূরক এনকোডিং কেন এবং কিভাবে কাজ করে?

যদি আমি আপনাকে একটি সংখ্যার ঋণাত্মক খুঁজে বের করতে বলি, +42 বলুন, +42-এর ঋণাত্মক খুঁজে বের করার সহজ উপায় কী?

তর্কাতীতভাবে, সবচেয়ে সহজ উপায় হল 0 থেকে সংখ্যাটি বিয়োগ করা, তাই না? 0 - (+42) = -42 . যদি আমরা এটি পুনরাবৃত্তি করি, আমরা ধনাত্মক মান, 0 - (-42) = +42-এ ফিরে যাব . এই সমস্ত গণিত যা দুজনের পরিপূরক তৈরি করে।

আমরা 10000 করছি (0 দশমিকে যেহেতু বামতম 1 একটি ওভারফ্লো) বিয়োগ 0101 (+5)। আমরা 1011 পাই দুই এর পরিপূরক এনকোডিং-এ দশমিকে -5। বিয়োগ কিভাবে করা হয় তা উপেক্ষা করুন। সেটা গুরুত্বপূর্ণ নয়. দুজনের পরিপূরকের পিছনে অন্তর্দৃষ্টি বোঝা গুরুত্বপূর্ণ।

10000 1111 + 0001 হিসাবে লেখা যেতে পারে (এই দুটি যোগ করার চেষ্টা করুন, আপনি 10000 পাবেন ) তাই আসলে আমরা করছি:

        10000       -   0101
=>  (1111 + 0001)   -   0101

উপরের সমীকরণটি পুনর্বিন্যাস করে আমরা এটিকে এভাবে লিখতে পারি:

    (1111 + 0001)  -  0101
=>  (1111 - 0101)  +  0001

Step 1: subtract 0101 from 1111

        1 1 1 1
       -0 1 0 1
       ---------
        1 0 1 0
        
       see, subtracting 0101 from 1111 is equivalent 
       to inverting the bits of 0101, as we got 1010 as a result. 

  
       
Step 2: add 0001 to the above result  

        1 0 1 0  ---> result of step 1
       +0 0 0 1
       ---------
        1 0 1 1      
       
       we get 1011 that is -5 in two's complement encoding.      

আপনি কি দেখেছেন যে দুটির পরিপূরক সিস্টেম মৌলিকভাবে 0 বিয়োগ সংখ্যা করে? বিটগুলি উল্টানো এবং একটি যোগ করা 0 থেকে সংখ্যা বিয়োগ করার একটি দ্রুত এবং চতুর উপায়৷

এই কারণেই আমরা একটি ধনাত্মক সংখ্যার ধনাত্মক এবং একটি ধনাত্মক সংখ্যার ঋণাত্মক পাই যখন আমরা এর দুটি পরিপূরক গণনা করি - কারণ আমরা আসলে 0 (0 - number) থেকে সংখ্যাটি বিয়োগ করছি। )

1900-এর দশকের কম্পিউটারগুলিতে শুধুমাত্র যোগ গাণিতিক যুক্তি ছিল কারণ দুটির পরিপূরক এনকোডিং স্কিম এত সুন্দর যে বিয়োগ সহজেই করা যেতে পারে।

উদাহরণস্বরূপ, 100 থেকে 12 বিয়োগ করতে, CPU দুইটির +12 এর পরিপূরক গণনা করে যা -12 উৎপন্ন করে তারপর আমরা -12 থেকে 100 যোগ করি যা আমাদের প্রয়োজনীয় আউটপুট দেয়।

কেন আমরা সরাসরি 0 থেকে বিয়োগ করি না বাইনারিতে একটি সংখ্যার নেতিবাচক বা বিপরীতে খুঁজে পেতে?

কারণ বিয়োগ একটি ধীর এবং জটিল প্রক্রিয়া (ধার নেওয়ার জন্য ধন্যবাদ) তাই আমাদের কম্পিউটারের একটি ব্যয়বহুল বিয়োগ বর্তনীর প্রয়োজন হবে যদি আমরা সেই পথে যাই। প্রতিবার যখন আমরা একটি ঋণাত্মক পূর্ণসংখ্যা উপস্থাপন করতে চাই তখন 0 থেকে বিয়োগ করার কল্পনা করুন। এটা আমাদের জন্য এবং আমাদের কম্পিউটারের জন্যও দুঃস্বপ্ন হবে!

দুটির পরিপূরক এনকোডিং একটি আরও কার্যকরী সমাধান, একটি সাধারণ সার্কিট ডিজাইনের দিকে নিয়ে যায় এবং প্রচুর অর্থ সাশ্রয় করে৷ কারণ বিয়োগের জন্য আমাদের কোনো ব্যয়বহুল সার্কিটের প্রয়োজন নেই এবং + এবং - পূর্ণসংখ্যার পাটিগণিতের সাথে মোকাবিলা করার জন্য কোনো অতিরিক্ত যুক্তি নেই। শুধু সরল যোগ এবং আমরা উভয়ই করতে পারি - যোগ এবং বিয়োগ।

তাই আসুন এই সুন্দর এনকোডিং স্কিমের জন্য আমাদের কম্পিউটার ডিজাইনারদের প্রশংসা করি – দুইটির পরিপূরক ❤️।

অন্তিম শব্দ

আমি নিজেকে প্রতিশ্রুতি দিয়েছিলাম যে আমার তৈরি করা কোনো শিক্ষার উপাদানের জন্য আমি কখনই চার্জ নেব না। আমি শিক্ষার জন্য যাই করি না কেন, তা একটি সাধারণ নিবন্ধ হোক বা একটি কোর্স বা একটি ইবুক, সর্বদা 100% বিনামূল্যে এবং উন্মুক্ত থাকবে৷

আমি দরকারী সম্পদ পোস্ট করি এবং আমার টুইটার অ্যাকাউন্টে অর্থপূর্ণ চিন্তা শেয়ার করি। আপনি আমাকে সেখানে অনুসরণ করতে পারেন এবং যদি আপনি এই নিবন্ধটি থেকে নতুন কিছু শিখেন তবে আমাকে একটি DM পাঠাতে পারেন। এটা আমার দিন তৈরি করবে :)

প্রতিটি বিকাশকারী, প্রতিটি লেখক এবং প্রতিটি মানুষই কারও না কারও কাছ থেকে শেখে। আমি বিশ্বাস করি যে মানুষ এবং সংস্থানগুলি থেকে আমরা শিখি তা উদ্ধৃত করা এবং ছড়িয়ে দেওয়া উচিত। এটি সেই ভালোদেরকে আমাদের সবার জন্য আরও কিছু করতে উৎসাহিত করে। তাই এখানে আমার ভাল আছে.

মাইকোডস্কুলের অনিমেষ আমাকে অনেকগুলি প্রোগ্রামিং ধারণা শিখিয়েছে যা আমি এই নিবন্ধে লিখেছি এমন ধারণাগুলি সহ অন্য কারও চেয়ে ভাল।

আন্দ্রে জেনিশ, আমার পরামর্শদাতা এবং বন্ধু, তার পর্যালোচনা প্রচেষ্টা এবং অবিরাম সমর্থন ছাড়া আমি এই নিবন্ধটি লিখতাম না।

সুখী শেখা!