রুবির সাথে বিগ-ও স্বরলিপি অন্বেষণ

একবার এমন একটি সময় ছিল যখন প্রশ্ন শোনার চেয়ে আর কিছুই আমাকে ভয় পেত না, "এর জন্য বিগ-ও স্বরলিপি কী?" আমি স্কুলের বিষয়টা মনে রেখেছিলাম, কিন্তু কারণ এটি গণিতের সাথে সম্পর্কিত ছিল (যেটি কখনই আমার সবচেয়ে শক্তিশালী বিষয় ছিল না), আমি এটি কালো করে দিয়েছিলাম।

যাইহোক, আমার ক্যারিয়ার যত এগিয়েছে, আমি নিজেকে খুঁজে পেয়েছি:

• পারফরম্যান্স চার্ট দেখছি
• ধীরগতির প্রশ্নগুলি ডিবাগ করার চেষ্টা করা হচ্ছে
• জিজ্ঞাসা করা হচ্ছে যে আমি বিবেচনা করেছি যে আমার কোড কিভাবে বর্ধিত লোড ধরে রাখবে

যখন আমি সিদ্ধান্ত নিলাম যে বিগ-ও শেখার জন্য বৃত্তাকারে ফিরে যাওয়ার (এটি পেতে?) সময় এসেছে, তখন আমি এর উচ্চ-স্তরের সরলতায় অবাক হয়েছিলাম। আমি এই নিবন্ধে যা শিখেছি তা শেয়ার করছি যাতে আপনি, আমার সহকর্মী প্রকৌশলীরা, শুধুমাত্র উড়ন্ত রঙের সাথে সাক্ষাত্কারে উত্তীর্ণ হতে পারেন না, কিন্তু পারফরম্যান্ট, স্কেলযোগ্য সিস্টেমও তৈরি করতে পারেন।

আমি প্রতিশ্রুতি দিচ্ছি, বিগ-ও ততটা ভীতিকর নয় যতটা মনে হচ্ছে। একবার আপনি এটি নামিয়ে ফেললে, আপনি একটি অ্যালগরিদম দেখতে পারেন এবং প্রোফাইলিং টুল চালানো ছাড়াই সহজেই এর কার্যকারিতা বুঝতে পারবেন!

বিগ-ও স্বরলিপি কি?

Big-O স্বরলিপি বলতে একটি অভিনব উপায়, "আরে, এই অ্যালগরিদমের জন্য সবচেয়ে খারাপ কেস পারফরম্যান্স কী?" আপনি O(n) বা O(1) হিসাবে বর্ণিত একটি ফাংশন দেখে থাকতে পারেন। এর মানে হল:

• O(n) - ইনপুট আকার (n) বাড়ার সাথে সাথে সবচেয়ে খারাপ-কেস রান টাইম রৈখিকভাবে বৃদ্ধি পায়
• O(1) - সবচেয়ে খারাপ-কেস রান টাইম যে কোনো আকারের ইনপুটের জন্য ধ্রুবক

...এবং এর অর্থ কী তা বোঝার জন্য, আমাদের অ্যাসিম্পটোটস সম্পর্কে শিখতে হবে

Asymptotes?

আসুন হাই স্কুল বীজগণিতে ফিরে যাই, আমাদের পাঠ্যপুস্তকটি ধুলোয় ফেলে দেই এবং সীমা এবং উপসর্গের অধ্যায়গুলিতে এটি খুলি৷

• সীমা বিশ্লেষণ: একটি ফাংশন যখন কিছু মানের কাছে আসে তখন তার কী ঘটে তা দেখা
• অ্যাসিম্পোটিক বিশ্লেষণ: f(x) অনন্তের কাছে আসার সাথে সাথে কী ঘটবে তা দেখছি

উদাহরণস্বরূপ, ধরা যাক আমরা f(x) =x^2 + 4x ফাংশনটি প্লট করি।

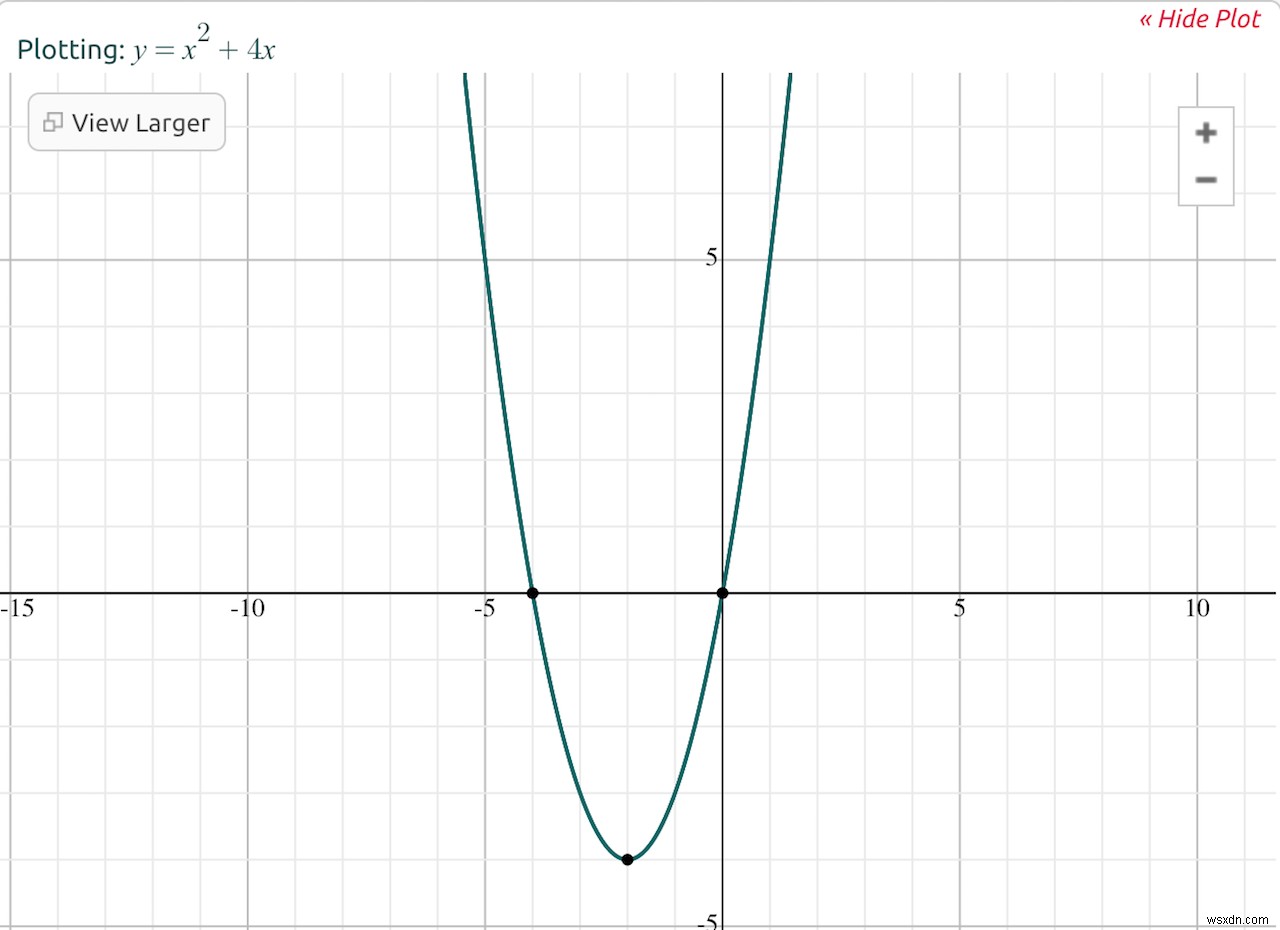
আমরা নিম্নলিখিত বিশ্লেষণগুলি সম্পাদন করতে পারি:- সীমা বিশ্লেষণ: x বাড়ার সাথে সাথে f(x) অসীমের কাছে আসে, তাই আমরা বলতে পারি যে f(x) =x^2 + 4x এর সীমা যখন x অসীমের কাছে আসে অসীমতা। - অ্যাসিম্পোটিক বিশ্লেষণ: যেহেতু x খুব বড় হয়ে যায়, x^2 পদের তুলনায় 4x পদটি তুচ্ছ হয়ে যায়। তাই আমরা বলতে পারি যে f(x) =x^2 + 4x প্রায় সমতুল্য হয়ে যায় f(x) =x^2 এর কাছে আসা অসীমতার মানের জন্য।

আমরা কীভাবে বলতে পারি যে একটি ফাংশনের অংশ "তুচ্ছ" হয়ে যায় তা বোঝার জন্য, আপনি যখন মূল ফাংশনে বিভিন্ন সংখ্যা প্লাগ করেন তখন কী হয় তা বিবেচনা করুন। উদাহরণস্বরূপ, যখন x =1, ফাংশনটি 1 + 4 প্রদান করে (যা 5 এর সমান)। যাইহোক, যখন x =2,000, ফাংশনটি 4,000,000 + 8,000 প্রদান করে (যা 4,008,000 এর সমান) -- x^2 শব্দটি 4x এর তুলনায় মোটে অনেক বেশি অবদান রাখে।

বিগ-ও নোটেশন হল ইনপুটের আকার পরিবর্তনের সাথে সাথে অ্যালগরিদমের রান টাইম কীভাবে পরিবর্তিত হয় তা বর্ণনা করার একটি উপায়।

একটি অ্যালগরিদমের রান টাইম কী নির্ধারণ করে?

আমি যদি আপনাকে জিজ্ঞাসা করি যে একটি খড়ের গাদায় একটি সুই খুঁজে পেতে আপনার কতক্ষণ লাগবে, আমি কল্পনা করি আপনি জানতে চাইবেন স্তুপে কতটা খড় রয়েছে। আমি যদি "10 টুকরা" উত্তর দিই তবে আমি বাজি ধরতে পারি আপনি বেশ আত্মবিশ্বাসী হবেন যে আপনি এক বা দুই মিনিটের মধ্যে সুইটি খুঁজে পেতে পারেন, কিন্তু যদি আমি বলি "1,000 টুকরা" তাহলে আপনি সম্ভবত ততটা উত্তেজিত হবেন না।

আরও একটি তথ্য আপনার জানা উচিত। খড়ের প্রতিটি খড়ের জন্য স্ট্যাক অনুসন্ধান করতে কতক্ষণ সময় লাগে? এবং খড়ের পরিমাণ অসীম হওয়ার সাথে সাথে কী ঘটে?

এটি উপরের অ্যাসিম্পোটিক বিশ্লেষণের উদাহরণের সাথে খুব মিল। আসুন আরও একটি উদাহরণ দেখি তা নিশ্চিত করার জন্য যে আমরা এটি সব নিচে পেয়েছি। ফাংশনটি বিবেচনা করুন f(x) =5x^2 + 100x + 50। আমরা এই ফাংশনের দুটি অংশ আলাদাভাবে প্লট করতে পারি:

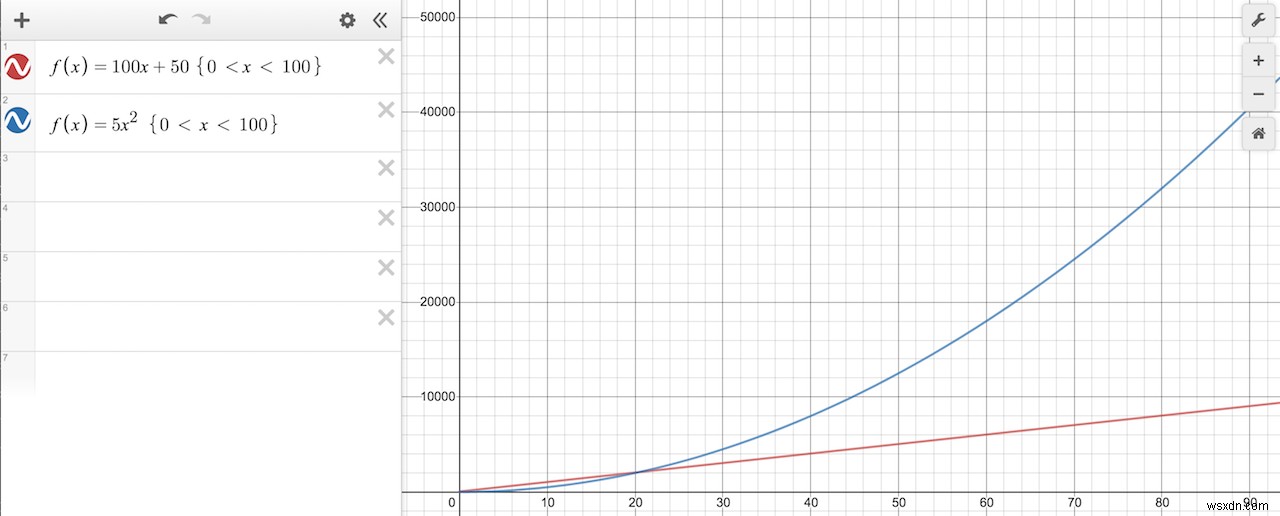
ঠিক আগের উদাহরণের মতো, 5x^2 শব্দটি অবশেষে 100x + 50 পদের চেয়ে বড় হয়ে যায়, তাই আমরা সেগুলি বাদ দিতে পারি এবং বলতে পারি যে f(x) =5x^2 + 100x + 50 এর রানটাইম x^2 হিসাবে বৃদ্ধি পায়।

অবশ্যই, এটি উল্লেখ করার মতো যে রান টাইমকে প্রভাবিত করে এমন অন্যান্য কারণ রয়েছে, যেমন প্রোগ্রাম চালানোর প্রকৃত কম্পিউটারের গতি এবং ব্যবহৃত ভাষা।

রৈখিক অনুসন্ধানের জন্য Big-O খোঁজা

আসুন লিনিয়ার সার্চ অ্যালগরিদমের একটি বিগ-ও বিশ্লেষণ করি। একটি রৈখিক অনুসন্ধান একটি ডেটাসেটের শুরুতে শুরু হয় এবং লক্ষ্য উপাদানটি না পাওয়া পর্যন্ত অতিক্রম করে৷

এখানে রুবি একটি বাস্তবায়ন.

def find_number_via_linear_search(array, target)
  counter = 0 

  # iterate through the given array starting 
  # at index 0 and continuing until the end 
  while counter < array.length 
    if array[counter] == target 
      # exit if target element found 
      return "linear search took: #{counter} iterations" 
    else 
      counter += 1 
    end 
  end 

  return "#{target} not found" 
end 

আমরা এই পদ্ধতিটিকে এভাবে একটি স্পিন দিতে পারি:

# Let's create an array with 50 integers
# and then re-arrange the order to make
# things more interesting
array = [*1..50].shuffle 

find_number_via_linear_search(array, 24)

আমি এটি কয়েকবার চালিয়েছি এবং নিম্নলিখিত ফলাফল পেয়েছি:

=> "linear search took: 10 iterations"
=> "linear search took: 11 iterations"
=> "linear search took: 26 iterations"

একটি ফাংশনের বিগ-ও স্বরলিপি বিশ্লেষণ করার সময়, আমরা সবচেয়ে খারাপ-কেস সিনরিও (ওরফে উপরের অ্যাসিম্পোটিক বাউন্ড) সম্পর্কে যত্ন নিই।

এটি সম্পর্কে স্বজ্ঞাতভাবে চিন্তা করলে, পুনরাবৃত্তির ক্ষুদ্রতম সংখ্যা হবে 1। এটি ঘটে যখন লক্ষ্য উপাদানটি অ্যারেতে 0 অবস্থানে ছিল। পুনরাবৃত্তির বৃহত্তম সংখ্যা (বা সবচেয়ে খারাপ-কেস দৃশ্যেরিও) হবে 50। এটি ঘটবে যখন লক্ষ্য উপাদানটি অ্যারেতে পাওয়া যায়নি।

যদি আমাদের অ্যারেতে 100টি উপাদান থাকে, তবে সবচেয়ে খারাপ ক্ষেত্রে 100টি পুনরাবৃত্তি হবে। 200 উপাদান? 200টি পুনরাবৃত্তি। এইভাবে, রৈখিক অনুসন্ধানের জন্য Big-O স্বরলিপি হল O(n), যেখানে n হল উপাদানের সংখ্যা।

বাইনারি অনুসন্ধানের সাথে আরও জটিল উদাহরণ!

এর পরে বাইনারি অনুসন্ধান বিবেচনা করা যাক. এখানে আপনি কিভাবে একটি প্রি-সর্টেড একটি বাইনারি অনুসন্ধান করবেন অ্যারে:1. মধ্যম উপাদান নিন
2. যদি element == target আমরা সম্পন্ন3. যদি element > target অ্যারের উপরের অর্ধেকটি বাতিল করুন 4. যদি element < target অ্যারের নিচের অর্ধেক বাদ দিন 5। ধাপ 1 থেকে বাকি অ্যারে দিয়ে আবার শুরু করুন

দ্রষ্টব্য:আপনি যদি একজন রুবিস্ট হন তবে একটি অন্তর্নির্মিত বি-সার্চ পদ্ধতি রয়েছে যা আপনার জন্য এই অ্যালগরিদমটি প্রয়োগ করে!

উদাহরণস্বরূপ, ধরা যাক যে আপনার একটি অভিধান আছে এবং আপনি বিশ্বের "আনারস" খুঁজছেন। আমরা অভিধানের মাঝের পৃষ্ঠায় যেতে চাই। এটা যদি বিশ্বের "আনারস" হয়েছে, আমরা সম্পন্ন হবে!

কিন্তু আমার অনুমান হল, অভিধানের মাঝামাঝি "p's" তে থাকবে না, তাই হয়তো আমরা "llama" শব্দটি খুঁজে পাব। "P" এর আগে "L" অক্ষরটি আসে তাই আমরা অভিধানের সম্পূর্ণ নীচের অর্ধেকটি বাতিল করে দেব। এর পরে, আমরা যা অবশিষ্ট আছে তা দিয়ে প্রক্রিয়াটি পুনরাবৃত্তি করব।

রৈখিক অনুসন্ধানের মতো, বাইনারি অনুসন্ধানের জন্য সেরা-কেস রান টাইম হল একটি পুনরাবৃত্তি। কিন্তু সবচেয়ে খারাপ কেস কি? এখানে 16টি উপাদান আছে এমন একটি উদাহরণ অ্যারে রয়েছে -- আসুন আমরা ভান করি যে আমরা 23 নম্বরটি খুঁজে পেতে একটি বাইনারি অনুসন্ধান ব্যবহার করতে চাই:

[2, 3, 15, 18, 22, 23, 24, 50, 65, 66, 88, 90, 92, 95, 100, 200]

প্রথম ধাপে সূচী 7-এ সংখ্যাটি দেখতে হবে, যা 50। যেহেতু 50 23-এর থেকে বড়, তাই আমরা ডানদিকে সবকিছু বাতিল করে দিই। এখন আমাদের অ্যারে দেখতে এইরকম:

[2, 3, 15, 18, 22, 23, 24, 50]

মাঝের উপাদানটি এখন 18, যা 23-এর থেকে কম, তাই আমরা এবার নিচের অর্ধেকটি বাতিল করে দিই।

[22, 23, 24, 50]

যা হয়ে যায়

[22, 23]

যা অবশেষে

[23]

মোট, আমরা অ্যারেতে যে সংখ্যাটি লক্ষ্য করেছিলাম তা খুঁজে বের করার জন্য আমাদের অ্যারেটিকে অর্ধেক 4 বার ভাগ করতে হয়েছিল, যার দৈর্ঘ্য ছিল 16৷

এটিকে সাধারণীকরণ করার জন্য, আমরা বলতে পারি যে বাইনারি অনুসন্ধানের জন্য সবচেয়ে খারাপ কেস সিনিরিও আমরা অ্যারেটিকে অর্ধেক ভাগ করতে পারি এমন সর্বোচ্চ সংখ্যার সমান।

গণিতে, আমরা এই প্রশ্নের উত্তর দিতে লগারিদম ব্যবহার করি, "আমরা এই সংখ্যাটির কতগুলি সংখ্যাটি পেতে পারি?" এখানে আমরা কিভাবে আমাদের সমস্যায় লগারিদম প্রয়োগ করি:

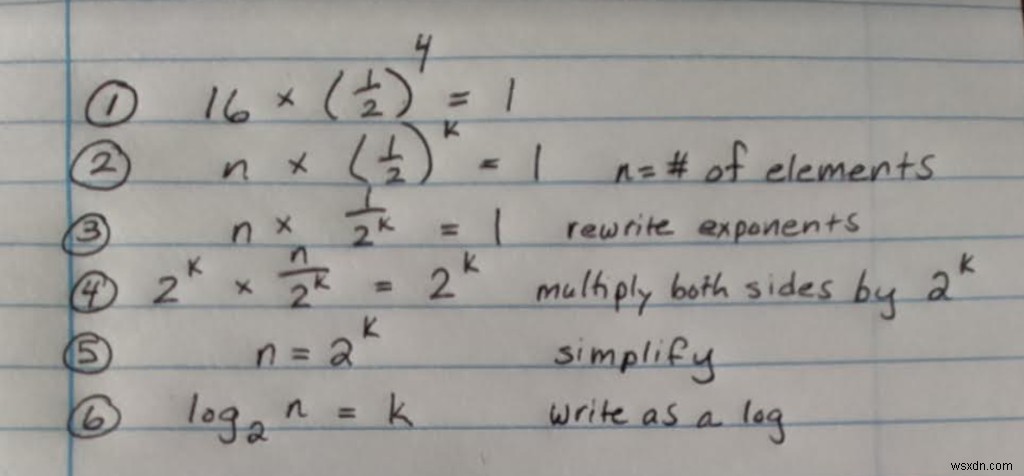
এইভাবে আমরা বলতে পারি যে বিগ-ও, বা বাইনারি অনুসন্ধানের জন্য সবচেয়ে খারাপ-কেস রান টাইম হল লগ(বেস 2) n।

র্যাপিং আপ

বিগ-ও স্বরলিপি বলতে একটি অভিনব উপায়, "আরে, এর জন্য সবচেয়ে খারাপ কেস কি?" কম্পিউটার বিজ্ঞানকে একপাশে রেখে, একটি বাস্তব-বিশ্বের উদাহরণ হতে পারে যখন আপনি আপনার প্লাম্বারকে জিজ্ঞাসা করেন যে ভাঙা কলটি মেরামত করতে কত খরচ হবে। তিনি উত্তর দিতে পারেন, "ঠিক আছে, আমি গ্যারান্টি দিতে পারি এটি $ 2,000 এর বেশি হবে না।" এটি একটি উচ্চ সীমা, যদিও আপনার জন্য খুব সহায়ক নয়।

এই কারণে, অন্যান্য বিগ-ও স্বরলিপিগুলি প্রায়শই ব্যবহার করা হয়। উদাহরণস্বরূপ, বিগ-থেটা নিম্ন আবদ্ধ এবং উপরের সীমা উভয়েরই যত্ন নেয়। এই ক্ষেত্রে, প্লাম্বার উত্তর দেবে, "ঠিক আছে, এটি $1,000 এর কম হবে না কিন্তু এটি $2,000 এর বেশি হবে না।" এটি অনেক বেশি দরকারী।

পড়ার জন্য আপনাকে ধন্যবাদ, এবং আমি আশা করি যে এই পোস্টটি বিগ-ও স্বরলিপি অন্তত একটি সামান্য কম ভীতিকর বিষয় করতে সাহায্য করেছে!