বিবেচনা করুন আমরা পয়েন্ট একটি সেট আছে. আমাদের একটি সহজ বদ্ধ পথ খুঁজে বের করতে হবে যা সমস্ত পয়েন্ট কভার করে। ধরুন বিন্দুগুলি নীচের মত, এবং পরবর্তী চিত্রটি সেই পয়েন্টগুলিতে একটি বন্ধ পথ তৈরি করছে৷
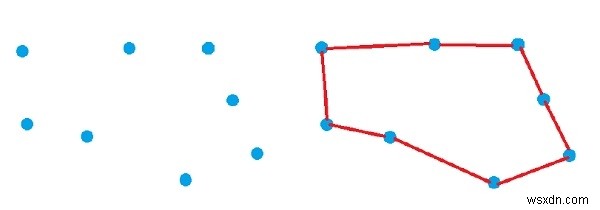
পথ পেতে, আমাদের এই ধাপগুলি অনুসরণ করতে হবে -
-
P
হিসাবে নীচের বাম বিন্দু খুঁজুন -
P এর চারপাশে ঘড়ির কাঁটার বিপরীত দিকে মেরু কোণের উপর ভিত্তি করে অন্যান্য n – 1 পয়েন্ট বাছাই করুন, যদি দুটি বিন্দুর মেরু কোণ একই হয়, তাহলে দূরত্ব সবচেয়ে কম বলে সেগুলিকে রাখুন
-
পয়েন্টের সাজানো তালিকা অতিক্রম করুন, তারপর পথ তৈরি করুন
উদাহরণ
#include <bits/stdc++.h>
using namespace std;
class Point {
public:
int x, y;
};
Point p0;
int euclid_dist(Point p1, Point p2) {
return (p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y);
}
int orientation(Point p1, Point p2, Point p3) {
int val = (p2.y - p1.y) * (p3.x - p2.x) - (p2.x - p1.x) * (p3.y - p2.y);
if (val == 0) return 0; // colinear
return (val > 0)? 1: 2; // clockwise or counterclock wise
}
int compare(const void *vp1, const void *vp2) {
Point *p1 = (Point *)vp1;
Point *p2 = (Point *)vp2;
int o = orientation(p0, *p1, *p2);
if (o == 0)
return (euclid_dist(p0, *p2) >= euclid_dist(p0, *p1))? -1 : 1;
return (o == 2)? -1: 1;
}
void findClosedPath(Point points[], int n) {
int y_min = points[0].y, min = 0;
for (int i = 1; i < n; i++) {
int y = points[i].y;
if ((y < y_min) || (y_min == y && points[i].x < points[min].x))
y_min = points[i].y, min = i;
}
swap(points[0], points[min]);
p0 = points[0];
qsort(&points[1], n-1, sizeof(Point), compare); //sort on polar angle
for (int i=0; i<n; i++)
cout << "(" << points[i].x << ", "<< points[i].y <<"), ";
}
int main() {
Point points[] = {{0, 3}, {1, 1}, {2, 2}, {4, 4},{0, 0}, {1, 2}, {3, 1}, {3, 3}};
int n = sizeof(points)/sizeof(points[0]);
findClosedPath(points, n);
} আউটপুট
(0, 0), (3, 1), (1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (0, 3),


