C++ ব্যবহার করে প্রদত্ত বিন্দু থেকে সম্ভাব্য চতুর্ভুজের সংখ্যা নির্ণয় করুন

ইউক্লিডীয় সমতল জ্যামিতিতে একটি চতুর্ভুজ চারটি শীর্ষবিন্দু এবং চারটি প্রান্ত সহ একটি বহুভুজ গঠন করে। নাম 4-gon ইত্যাদি। চতুর্ভুজের অন্যান্য নামের অন্তর্ভুক্ত এবং কখনও কখনও এগুলি একটি বর্গক্ষেত্র, প্রদর্শন শৈলী ইত্যাদি নামেও পরিচিত।

এই নিবন্ধে, আমরা প্রদত্ত বিন্দুগুলি থেকে সম্ভাব্য চতুর্ভুজের সংখ্যা খুঁজে বের করার পদ্ধতিগুলি ব্যাখ্যা করব। এই সমস্যায়, কার্টেসিয়ান সমতলে প্রদত্ত চারটি বিন্দু (x, y) দিয়ে কতগুলি সম্ভাব্য চতুর্ভুজ তৈরি করা সম্ভব তা খুঁজে বের করতে হবে। তাই এখানে প্রদত্ত সমস্যার উদাহরণ −

Input : A( -2, 8 ), B( -2, 0 ), C( 6, -1 ), D( 0, 8 )
Output : 1
Explanation : One quadrilateral can be formed ( ABCD )

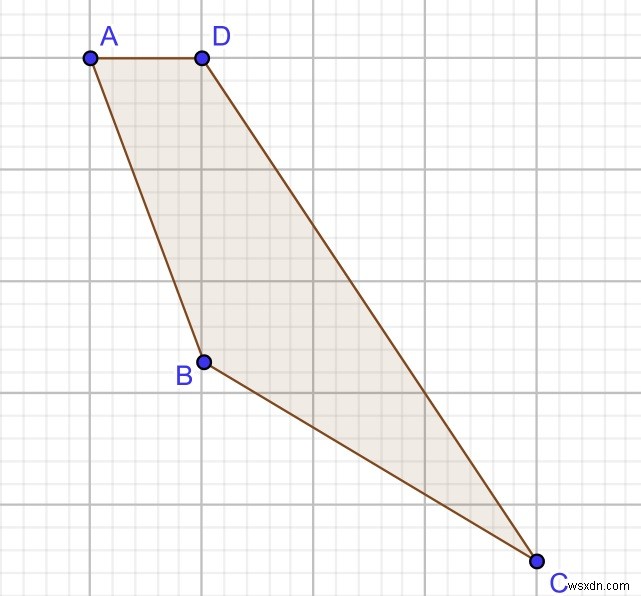
Input : A( 1, 8 ), B( 0, 1 ), C( 4, 0 ), D( 1, 2 )
Output : 3
Explanation : 3 quadrilaterals can be formed (ABCD), (ABDC) and (ADBC).

সমাধান খোঁজার পদ্ধতি

• আমরা প্রথমে পরীক্ষা করব যে 4টির মধ্যে 3টি বিন্দু সমরৈখিক কিনা এবং যদি হ্যাঁ হয়, তাহলে বিন্দু দিয়ে কোনো চতুর্ভুজ তৈরি করা যাবে না .

• এর পরে, আমরা পরীক্ষা করব যে 4 বিন্দুর মধ্যে 2টি একই কিনা এবং যদি হ্যাঁ, তাহলে কোন চতুর্ভুজ গঠন করা যাবে না .

• এখন, আমরা তির্যকটি ছেদ করে কিনা তা পরীক্ষা করব। যদি হ্যাঁ, তাহলে শুধুমাত্র একটি সম্ভাব্য চতুর্ভুজ গঠিত হতে পারে, যাকে বলা হয় একটি উত্তল চতুর্ভুজ .

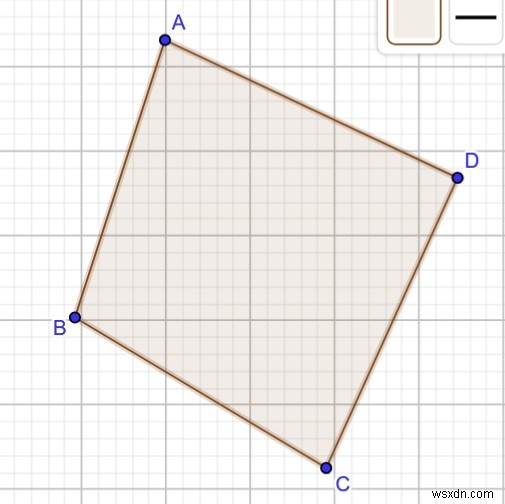
মোট ছেদ সংখ্যা =1

যদি কর্ণগুলি ছেদ না করে, তাহলে তিনটি সম্ভাব্য চতুর্ভুজ তৈরি হতে পারে, যাকে অবতল চতুর্ভুজ বলা হয়।

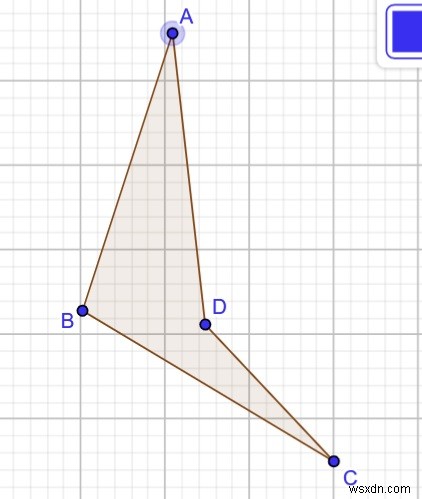
মোট ছেদ সংখ্যা =0

উদাহরণ

#include <iostream>
using namespace std;
struct Point{ // points
    int x;
    int y;
};
int check_orientation(Point i, Point j, Point k){
    int val = (j.y - i.y) * (k.x - j.x) - (j.x - i.x) * (k.y - j.y);
    if (val == 0)
       return 0;
    return (val > 0) ? 1 : 2;
}
// checking whether line segments intersect
bool check_Intersect(Point A, Point B, Point C, Point D){
    int o1 = check_orientation(A, B, C);
    int o2 = check_orientation(A, B, D);
    int o3 = check_orientation(C, D, A);
    int o4 = check_orientation(C, D, B);
    if (o1 != o2 && o3 != o4)
       return true;
    return false;
}
// checking whether 2 points are same
bool check_similar(Point A, Point B){
   // If found similiar then we are returning false that means no quad. can be formed
    if (A.x == B.x && A.y == B.y)
       return false;
   // returning true for not found similiar
    return true;
}
// Checking collinearity of three points
bool check_collinear(Point A, Point B, Point C){
    int x1 = A.x, y1 = A.y;
    int x2 = B.x, y2 = B.y;
    int x3 = C.x, y3 = C.y;
    if ((y3 - y2) * (x2 - x1) == (y2 - y1) * (x3 - x2))
       return false;
    else
       return true;
}
// main function
int main(){
   struct Point A,B,C,D;
   A.x = -2, A.y = 8;// A(-2, 8)
   B.x = -2, B.y = 0;// B(-2, 0)
   C.x = 6, C.y = -1;// C(6, -1)
   D.x = 0, D.y = 8;// D(0, 8)
   // Checking whether any 3 points are collinear
   bool flag = true;
   flag = flag & check_collinear(A, B, C);
   flag = flag & check_collinear(A, B, D);
   flag = flag & check_collinear(A, C, D);
   flag = flag & check_collinear(B, C, D);
   // If points found collinear
   if (flag == false){
       cout << "Number of quadrilaterals possible from the given points: 0";
       return 0;
   }
   // Checking if 2 points are same.
   bool same = true;
   same = same & check_similar(A, B);
   same = same & check_similar(A, C);
   same = same & check_similar(B, D);
   same = same & check_similar(C, D);
   same = same & check_similar(A, D);
   same = same & check_similar(B, C);
   // If similiar point exist
   if (same == false){
       cout << "Number of quadrilaterals possible from the given points: 0";
   return 0;
   }
   // checking whether diagonal intersect or not
    flag = true;
   if (check_Intersect(A, B, C, D))
       flag = false;
   if (check_Intersect(A, C, B, D))
       flag = false;
   if (check_Intersect(A, B, D, C))
       flag = false;
   if (flag == true)
       cout << "Number of quadrilaterals possible from the given points: 3";
   else
       cout << "Number of quadrilaterals possible from the given points: 1";
   return 0;
}

আউটপুট

Number of quadrilaterals possible from the given points : 1

উপরের কোডের ব্যাখ্যা

এই কোডটি নিম্নলিখিত ধাপে বোঝা যাবে −

• কোন তিনটি বিন্দু সমরেখার কিনা তা পরীক্ষা করা হচ্ছে এবং যদি হ্যাঁ হয়, তাহলে একটি চতুর্ভুজের সংখ্যা। :0

• যেকোনো দুটি বিন্দুর মিল আছে কিনা তা পরীক্ষা করা হচ্ছে এবং যদি হ্যাঁ, তাহলে একটি চতুর্ভুজের সংখ্যা। :0

• কোনো রেখার অংশ ছেদ করে কিনা তা পরীক্ষা করা হচ্ছে:

  • যদি হ্যাঁ হয়, তাহলে একটি কোয়াডের সংখ্যা। :1

  • যদি না হয়, তাহলে quads সংখ্যা. :3

উপসংহার

এই নিবন্ধে, আমরা প্রদত্ত 4টি বিন্দু থেকে গঠিত হতে পারে এমন সমস্ত সম্ভাব্য চতুর্ভুজ খুঁজে বের করেছি। আমরা বুঝতে পারি কিভাবে চতুর্ভুজের সংখ্যা সমকোনতা, ছেদ এবং অভিযোজনের উপর নির্ভর করে। আমরা এটির জন্য C++ প্রোগ্রামও লিখি, এবং আমরা এই প্রোগ্রামটিকে অন্য যেকোনো ভাষায় লিখতে পারি যেমন সি, জাভা এবং পাইথন।