এই সমস্যায়, আমাদের একটি বাইনারি গাছ বিটি দেওয়া হয়। আমাদের কাজ হল প্রদত্ত বাইনারি ট্রিতে সবচেয়ে বড় BST সাবট্রি খুঁজে পাওয়া .
বাইনারি ট্রি হল একটি বিশেষ ডেটা স্ট্রাকচার যা ডেটা স্টোরেজের উদ্দেশ্যে ব্যবহৃত হয়। একটি বাইনারি গাছের একটি বিশেষ শর্ত রয়েছে যে প্রতিটি নোডে সর্বাধিক দুটি শিশু থাকতে পারে৷
বাইনারি সার্চ ট্রি (বিএসটি) হল এমন একটি গাছ যেখানে সমস্ত নোড নীচের উল্লেখিত বৈশিষ্ট্যগুলি অনুসরণ করে -
-
বাম সাব-ট্রির কী-এর মান এর মূল (রুট) নোডের কী-এর মানের থেকে কম৷
-
ডান সাবট্রির কী-এর মান তার মূল (রুট) নোডের কী-এর মানের থেকে বেশি বা সমান৷
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক,
ইনপুট:
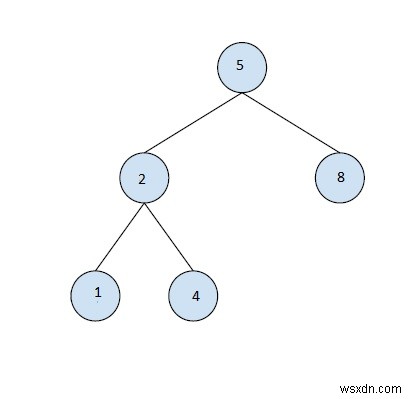
আউটপুট:3
ব্যাখ্যা
Full binary tree is a BST.
সমাধান পদ্ধতি
সমস্যার একটি সহজ সমাধান হল গাছের ইন-অর্ডার ট্রাভার্সাল করা। এবং গাছের প্রতিটি নোডের জন্য, এর সাবট্রিগুলি BST কিনা তা পরীক্ষা করুন। শেষ পর্যন্ত সবচেয়ে বড় সাবট্রির সাইজ দিন যা একটি BST।
উদাহরণ
আমাদের সমাধানের কাজ চিত্রিত করার জন্য প্রোগ্রাম
#include<bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node* left;
node* right;
node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
int findTreeSize(node* node) {
if (node == NULL)
return 0;
else
return(findTreeSize(node->left) + findTreeSize(node->right) + 1);
}
int isBSTree(struct node* node) {
if (node == NULL)
return 1;
if (node->left != NULL && node->left->data > node->data)
return 0;
if (node->right != NULL && node->right->data < node->data)
return 0;
if (!isBSTree(node->left) || !isBSTree(node->right))
return 0;
return 1;
}
int findlargestBSTSize(struct node *root) {
if (isBSTree(root)){
return findTreeSize(root);
}
else
return max(findlargestBSTSize(root->left), findlargestBSTSize(root->right));
}
int main() {
node *root = new node(5);
root->left = new node(2);
root->right = new node(8);
root->left->left = new node(1);
root->left->right = new node(4);
cout<<"The size of the largest possible BST is "<<findlargestBSTSize(root);
return 0;
} আউটপুট
The size of the largest possible BST is 5
আরেকটি পদ্ধতি
সমস্যার আরেকটি সমাধান হল গাছটিকে নিচ থেকে ট্র্যাভার্স করা এবং এটির চাইল্ড নোড ব্যবহার করে এটি BST কিনা তা পরীক্ষা করা। এই নোডের জন্য, আমরা ট্র্যাক রাখব
যদি এটি একটি BST হয় বা না হয়।
-
বাম সাবট্রির ক্ষেত্রে সর্বাধিক উপাদানের মান।
-
ডান সাবট্রির ক্ষেত্রে নূন্যতম উপাদান। BST চেকের জন্য এই মানগুলি বর্তমান নোডের সাথে তুলনা করা দরকার।
এছাড়াও, বর্তমান BST আকারের সাথে চেক করে বৃহত্তম BST-এর আকার আপডেট করা হবে।
উদাহরণ
#include<bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node* left;
node* right;
node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
int findlargestBSTSizeRec(node* node, int *minValRsubTree, int *maxValLsubTree, int *maxBSTSize, bool *isBSTree) {
if (node == NULL){
*isBSTree = true;
return 0;
}
int min = INT_MAX;
bool left_flag = false;
bool right_flag = false;
int leftSubtreeSize,rightSubTreeSize;
*maxValLsubTree = INT_MIN;
leftSubtreeSize = findlargestBSTSizeRec(node->left, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
if (*isBSTree == true && node->data > *maxValLsubTree)
left_flag = true;
min = *minValRsubTree;
*minValRsubTree = INT_MAX;
rightSubTreeSize = findlargestBSTSizeRec(node->right, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
if (*isBSTree == true && node->data < *minValRsubTree)
right_flag = true;
if (min < *minValRsubTree)
*minValRsubTree = min;
if (node->data < *minValRsubTree)
*minValRsubTree = node->data;
if (node->data > *maxValLsubTree)
*maxValLsubTree = node->data;
if(left_flag && right_flag){
if (leftSubtreeSize + rightSubTreeSize + 1 > *maxBSTSize)
*maxBSTSize = (leftSubtreeSize + rightSubTreeSize + 1);
return (leftSubtreeSize + rightSubTreeSize + 1);
}
else{
*isBSTree = false;
return 0;
}
}
int findlargestBSTSize(node* node){
int min = INT_MAX;
int max = INT_MIN;
int largestBSTSize = 0;
bool isBST = false;
findlargestBSTSizeRec(node, &min, &max, &largestBSTSize, &isBST);
return largestBSTSize;
}
int main(){
node *root = new node(5);
root->left = new node(2);
root->right = new node(8);
root->left->left = new node(1);
root->left->right = new node(4);
cout<<"The Size of the largest BST is "<<findlargestBSTSize(root);
return 0;
} আউটপুট
The Size of the largest BST is 5


