এই সমস্যায়, আমাদের একটি 2-ডি অ্যারে দেওয়া হয়েছে যেখানে একটি n-ary এর প্রান্ত রয়েছে যেখানে প্রান্তটি n-ary গাছের প্রান্তকে সংজ্ঞায়িত করে। আমাদের তৈরি করা a-ary গাছের সমস্ত লিফ নোড প্রিন্ট করতে হবে।
এন-আরি গাছ এমন একটি গাছ যার সর্বাধিক n শিশু রয়েছে অর্থাৎ একটি নোডে 1, 2, ...n চাইল্ড নোড থাকতে পারে৷
আসুন সমস্যাটি বোঝার জন্য একটি উদাহরণ দেখি -
Input: edge[][] = {{5,8}, {5,6}, {8,1}, {8,4}, {6,7}}
Output: 1 4 7 ব্যাখ্যা - চলুন এজ অ্যারে -
ব্যবহার করে একটি ট্রি তৈরি করি
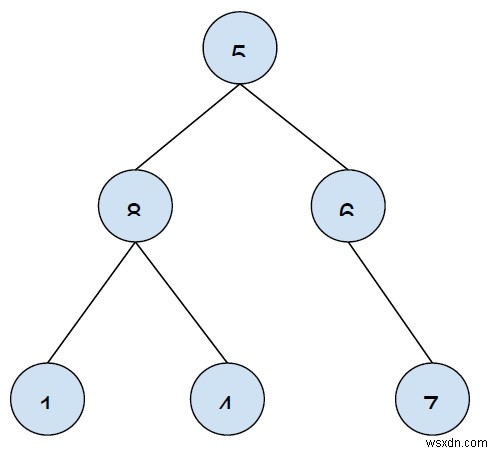
এই গাছের পাতার নোডগুলি হল 1, 4, 7৷
এই সমস্যাটি সমাধান করার জন্য, আমরা DFS ব্যবহার করে গাছটি অতিক্রম করব (এটি প্রতিটি সাবট্রির লিফ নোড খুঁজে পাবে)। এছাড়াও, অ্যারের পরিদর্শন করা নোডগুলি চিহ্নিত করা হয়েছে। যদি নোডের একটি শিশু থাকে (যদি লিফ নোড না হয়), তাহলে আমরা মান ফ্ল্যাগ করব এবং চাইল্ড নোড ছাড়াই নোড প্রিন্ট করব৷
উদাহরণ
এই প্রোগ্রামটি আমাদের সমাধানের বাস্তবায়ন দেখায় -
#include <bits/stdc++.h>
using namespace std;
void DFS(list<int> t[], int node, int parent) {
int flag = 0;
for (auto ir : t[node]) {
if (ir != parent) {
flag = 1;
DFS(t, ir, node);
}
}
if (flag == 0)
cout<<node<<"\t";
}
int main() {
list<int> t[1005];
pair<int, int> edges[] = {
{ 1, 2 },
{ 1, 3 },
{ 2, 4 },
{ 3, 5 },
{ 3, 6 },
{ 3, 7 },
{ 6, 8 }
};
int cnt = sizeof(edges) / sizeof(edges[0]);
int node = cnt + 1;
for (int i = 0; i < cnt; i++) {
t[edges[i].first].push_back(edges[i].second);
t[edges[i].second].push_back(edges[i].first);
}
cout<<"Leaf nodes of the tree are:\n";
DFS(t, 1, 0);
return 0;
} আউটপুট
Leaf nodes of the tree are − 4 5 8 7


