ধরুন আমাদের একটি বাইনারি ট্রি, একটি টার্গেট নোড এবং একটি মান K আছে। আমাদের লক্ষ্য নোড থেকে K দূরত্ব আছে এমন সমস্ত নোডের মানগুলির একটি তালিকা খুঁজে বের করতে হবে।
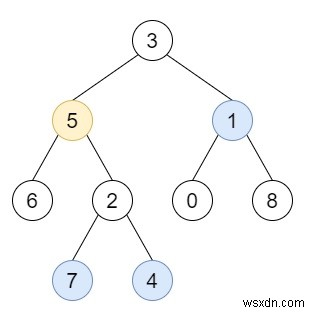
সুতরাং, যদি ইনপুটটি root =[3,5,1,6,2,0,8,null,null,7,4], target =5, K =2 এর মত হয়, তাহলে আউটপুট হবে [7,4] ,1], কারণ টার্গেট নোড থেকে 2 দূরত্বের নোডগুলির মান 7, 4 এবং 1 আছে৷
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
একটি ফাংশন dfs() সংজ্ঞায়িত করুন, এটি নোড নেবে, pa এটিকে NULL দিয়ে আরম্ভ করুন,
-
যদি নোড নাল হয়, তাহলে −
-
ফেরত
-
-
অভিভাবক [নোড] :=pa
-
dfs(নোডের বামে, নোড)
-
dfs(নোডের ডান, নোড)
-
প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
-
একটি অ্যারে উত্তর সংজ্ঞায়িত করুন
-
dfs(root)
-
(নোড, মান) জোড়া
এর জন্য একটি সারি q সংজ্ঞায়িত করুন -
q
-এ { target, 0 } ঢোকান -
পরিদর্শন বলে একটি সেট সংজ্ঞায়িত করুন
-
পরিদর্শন
এ লক্ষ্য সন্নিবেশ করান -
যখন (q খালি নয়), −
করুন-
এক জোড়া সংজ্ঞায়িত করুন p :=q এর প্রথম উপাদান
-
q
থেকে উপাদান মুছুন -
স্তর :=তাপমাত্রার দ্বিতীয় উপাদান
-
নোড =তাপমাত্রার প্রথম উপাদান।
-
যদি স্তর k এর সমান হয়, তাহলে −
-
উত্তরের শেষে নোডের মান সন্নিবেশ করুন
-
-
যদি নোডের বাম অংশ নাল না হয় এবং স্তর + 1 <=k এবং নোডের বাম অংশ পরিদর্শন না করা হয়, তাহলে
-
q
-এ {নোডের বামে, স্তর + 1 }) সন্নিবেশ করুন -
পরিদর্শন করা সেটে নোডের বাম দিকে ঢোকান
-
-
যদি নোডের ডানদিকে শূন্য না হয় এবং স্তর + 1 <=k এবং নোডের ডানদিকে পরিদর্শন না করা হয়, তাহলে
-
q
-এ {নোডের ডানদিকে, স্তর + 1 }) সন্নিবেশ করুন -
ভিজিট করা সেটে নোডের ডানদিকে সন্নিবেশ করুন
-
-
যদি প্যারেন্ট [নোড] NULL না হয় এবং স্তর + 1 <=k এবং প্যারেন্ট[নোড] পরিদর্শন না করা হয়, তাহলে -
-
q
-এ { প্যারেন্ট[নোড], লেভেল + 1 } সন্নিবেশ করুন -
ভিজিটেড
-এ প্যারেন্ট[নোড] সন্নিবেশ করুন
-
-
-
উত্তর ফেরত দিন
উদাহরণ
আরো ভালোভাবে বোঝার জন্য নিচের বাস্তবায়নটি দেখি -
#include <bits/stdc++.h>
using namespace std;
void print_vector(vector<int> v){
cout << "[";
for(int i = 0; i<v.size(); i++){
cout << v[i] << ", ";
}
cout << "]"<<endl;
}
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
void insert(TreeNode **root, int val){
queue<TreeNode*> q;
q.push(*root);
while(q.size()){
TreeNode *temp = q.front();
q.pop();
if(!temp->left){
if(val != NULL)
temp->left = new TreeNode(val);
else
temp->left = new TreeNode(0);
return;
}else{
q.push(temp->left);
}
if(!temp->right){
if(val != NULL)
temp->right = new TreeNode(val);
else
temp->right = new TreeNode(0);
return;
}else{
q.push(temp->right);
}
}
}
TreeNode *make_tree(vector<int> v){
TreeNode *root = new TreeNode(v[0]);
for(int i = 1; i<v.size(); i++){
insert(&root, v[i]);
}
return root;
}
class Solution {
public:
map <TreeNode*, TreeNode*> parent;
void dfs(TreeNode* node, TreeNode* pa = NULL){
if (!node)
return;
parent[node] = pa;
dfs(node->left, node);
dfs(node->right, node);
}
vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {
vector<int> ans;
parent.clear();
dfs(root);
queue<pair<TreeNode*, int> > q;
q.push({ target, 0 });
set<TreeNode*> visited;
visited.insert(target);
while (!q.empty()) {
pair<TreeNode*, int> temp = q.front();
q.pop();
int level = temp.second;
TreeNode* node = temp.first;
if (level == k) {
ans.push_back(node->val);
}
if ((node->left && node->left->val != 0) && level + 1 <= k && !visited.count(node->left)) {
q.push({ node->left, level + 1 });
visited.insert(node->left);
}
if ((node->right && node->right->val != 0) && level + 1 <= k && !visited.count(node->right)){
q.push({ node->right, level + 1 });
visited.insert(node->right);
}
if (parent[node] != NULL && level + 1 <= k && !visited.count(parent[node])) {
q.push({ parent[node], level + 1 });
visited.insert(parent[node]);
}
}
return ans;
}
};
main(){
Solution ob;
vector<int> v = {3,5,1,6,2,0,8,NULL,NULL,7,4};
TreeNode *root = make_tree(v);
TreeNode *target = root->left;
print_vector(ob.distanceK(root, target, 2));
} ইনপুট
{3,5,1,6,2,0,8,NULL,NULL,7,4} আউটপুট
[7, 4, 1, ]


