এই সমস্যায়, আমাদের একটি বাইনারি সার্চ ট্রি দেওয়া হয়েছে এবং আমাদের বিজোড় মান আছে এমন সমস্ত নোড প্রিন্ট করতে হবে৷
বাইনারী অনুসন্ধান গাছ হল একটি বিশেষ ধরনের গাছ যা নিম্নলিখিত বৈশিষ্ট্য ধারণ করে -
-
বাম সাবট্রিতে সবসময় রুট নোডের চেয়ে ছোট মান থাকে।
-
ডান সাবট্রিতে সবসময় রুট নোডের চেয়ে বড় মান থাকে।
-
বাম এবং ডান উপবৃক্ষ উভয়ই উপরের দুটি বৈশিষ্ট্য অনুসরণ করা উচিত।
সমস্যাটি বোঝার জন্য একটি উদাহরণ নেওয়া যাক -
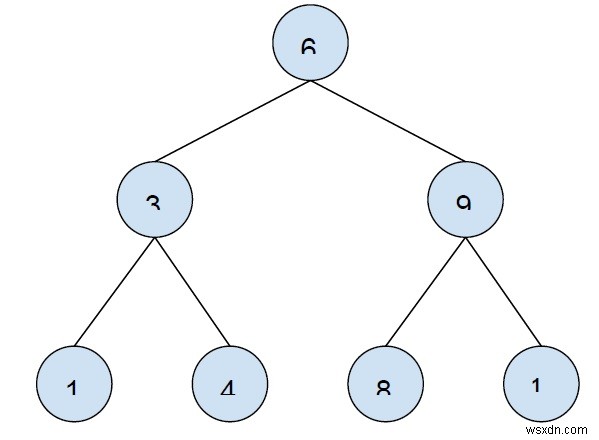
আউটপুট − 1 3 9
এই সমস্যাটি সমাধান করার জন্য, একটি সহজ পদ্ধতি গাছটি অতিক্রম করা হবে। ট্রাভার্সালে, আমরা গাছের প্রতিটি নোডের মান পরীক্ষা করব। নোড বিজোড় হলে গাছের পরবর্তী নোডে প্রিন্ট করুন।
প্রোগ্রামের জটিলতা নোডের সংখ্যার উপর নির্ভর করবে। সময় জটিলতা:O(n)।
উদাহরণ
নীচের প্রোগ্রামটি আমাদের সমাধানের বাস্তবায়ন দেখায় -
#include <bits/stdc++.h>
using namespace std;
struct Node {
int key;
struct Node *left, *right;
};
Node* newNode(int item){
Node* temp = new Node;
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
Node* insertNode(Node* node, int key){
if (node == NULL)
return newNode(key);
if (key < node->key)
node->left = insertNode(node->left, key);
else
node->right = insertNode(node->right, key);
return node;
}
void printOddNodes(Node* root){
if (root != NULL) {
printOddNodes(root->left);
if (root->key % 2 != 0)
cout<<root->key<<"\t";
printOddNodes(root->right);
}
}
int main(){
Node* root = NULL;
root = insertNode(root, 6);
root = insertNode(root, 3);
root = insertNode(root, 1);
root = insertNode(root, 4);
root = insertNode(root, 9);
root = insertNode(root, 8);
root = insertNode(root, 10);
cout<<"Nodes with odd values are :\n";
printOddNodes(root);
return 0;
} আউটপুট
বিজোড় মান সহ নোড হল −
1 3 9


