একটি বিস্তৃত গাছ এটি একটি অনির্দেশিত গ্রাফের একটি উপসেট যাতে ন্যূনতম সংখ্যক প্রান্ত দ্বারা সংযুক্ত সমস্ত শীর্ষবিন্দু রয়েছে৷
যদি সমস্ত শীর্ষবিন্দু একটি গ্রাফে সংযুক্ত থাকে, তাহলে অন্তত একটি বিস্তৃত গাছ রয়েছে। একটি গ্রাফে, একাধিক বিস্তৃত গাছ থাকতে পারে।
সর্বনিম্ন স্প্যানিং ট্রি
একটি মিনিমাম স্প্যানিং ট্রি (MST) একটি সংযুক্ত ওজনযুক্ত অনির্দেশিত গ্রাফের প্রান্তগুলির একটি উপসেট যা ন্যূনতম সম্ভাব্য মোট প্রান্তের ওজনের সাথে সমস্ত শীর্ষবিন্দুকে একত্রে সংযুক্ত করে। একটি MST প্রাপ্ত করার জন্য, Prim's Algorithm বা Kruskal's Algorithm ব্যবহার করা যেতে পারে। তাই, আমরা এই অধ্যায়ে প্রাইমের অ্যালগরিদম নিয়ে আলোচনা করব।
যেমনটি আমরা আলোচনা করেছি, একটি গ্রাফে একাধিক বিস্তৃত গাছ থাকতে পারে। যদি n থাকে শীর্ষবিন্দুর সংখ্যা, বিস্তৃত গাছের n - 1 থাকা উচিত প্রান্তের সংখ্যা। এই প্রসঙ্গে, যদি গ্রাফের প্রতিটি প্রান্ত একটি ওজনের সাথে যুক্ত থাকে এবং সেখানে একাধিক স্প্যানিং ট্রি থাকে, তাহলে আমাদের গ্রাফের ন্যূনতম স্প্যানিং ট্রি খুঁজে বের করতে হবে।
অধিকন্তু, যদি কোনো ডুপ্লিকেট ওজনযুক্ত প্রান্ত বিদ্যমান থাকে, তাহলে গ্রাফটিতে একাধিক ন্যূনতম স্প্যানিং ট্রি থাকতে পারে।
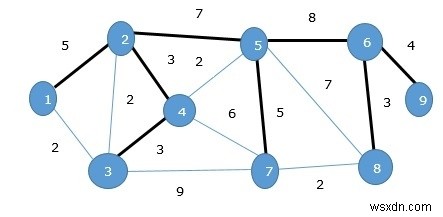
উপরের গ্রাফে, আমরা একটি বিস্তৃত গাছ দেখিয়েছি যদিও এটি সর্বনিম্ন বিস্তৃত গাছ নয়। এই বিস্তৃত গাছের দাম (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) =38।


