বাইনারি সার্চ ট্রি হল বাইনারি ট্রি যার কিছু বৈশিষ্ট্য আছে। এই বৈশিষ্ট্যগুলি নীচের মত -
- প্রতিটি বাইনারি সার্চ ট্রি একটি বাইনারি ট্রি
- প্রতিটি বাম শিশু মূলের চেয়ে কম মান ধারণ করবে
- প্রতিটি সঠিক শিশু মূলের চেয়ে বেশি মূল্য ধারণ করবে
- আদর্শ বাইনারি সার্চ ট্রি একই মান দুইবার ধরে রাখবে না।
ধরুন আমাদের এইরকম একটি গাছ আছে -
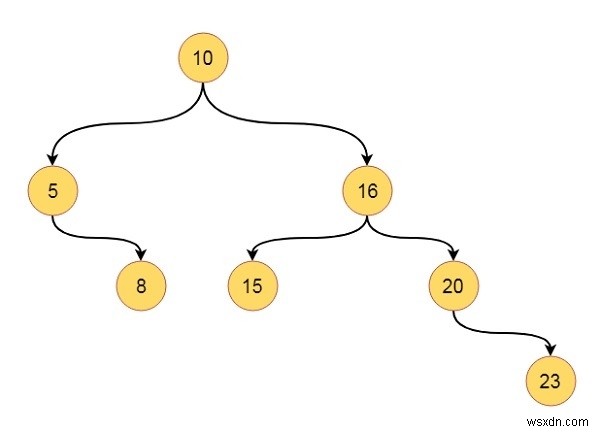
এই গাছ একটি বাইনারি অনুসন্ধান গাছ. এটি উল্লিখিত সমস্ত বৈশিষ্ট্য অনুসরণ করে। আমরা যদি উপাদানগুলিকে ইনঅর্ডার ট্রাভার্সাল মোডে অতিক্রম করি, তাহলে আমরা 5, 8, 10, 15, 16, 20, 23 পেতে পারি। C++ কোডে আমরা কীভাবে এটি বাস্তবায়ন করতে পারি তা বোঝার জন্য আসুন একটি কোড দেখি।
উদাহরণ
#include<iostream>
using namespace std;
class node{
public:
int h_left, h_right, bf, value;
node *left, *right;
};
class tree{
private:
node *get_node(int key);
public:
node *root;
tree(){
root = NULL; //set root as NULL at the beginning
}
void inorder_traversal(node *r);
node *insert_node(node *root, int key);
};
node *tree::get_node(int key){
node *new_node;
new_node = new node; //create a new node dynamically
new_node->h_left = 0; new_node->h_right = 0;
new_node->bf = 0;
new_node->value = key; //store the value from given key
new_node->left = NULL; new_node->right = NULL;
return new_node;
}
void tree::inorder_traversal(node *r){
if(r != NULL){ //When root is present, visit left - root - right
inorder_traversal(r->left);
cout << r->value << " ";
inorder_traversal(r->right);
}
}
node *tree::insert_node(node *root, int key){
if(root == NULL){
return (get_node(key)); //when tree is empty, create a node as root
}
if(key < root->value){ //when key is smaller than root value, go to the left
root->left = insert_node(root->left, key);
}else if(key > root->value){ //when key is greater than root value, go to the right
root->right = insert_node(root->right, key);
}
return root; //when key is already present, do not insert it again
}
main(){
node *root;
tree my_tree;
//Insert some keys into the tree.
my_tree.root = my_tree.insert_node(my_tree.root, 10);
my_tree.root = my_tree.insert_node(my_tree.root, 5);
my_tree.root = my_tree.insert_node(my_tree.root, 16);
my_tree.root = my_tree.insert_node(my_tree.root, 20);
my_tree.root = my_tree.insert_node(my_tree.root, 15);
my_tree.root = my_tree.insert_node(my_tree.root, 8);
my_tree.root = my_tree.insert_node(my_tree.root, 23);
cout << "In-Order Traversal: ";
my_tree.inorder_traversal(my_tree.root);
} আউটপুট
In-Order Traversal: 5 8 10 15 16 20 23


