ডেটা স্ট্রাকচারে হাফম্যান ট্রি

সংজ্ঞা

হাফম্যান কোডিং ক্যারেক্টারের রিলেটিভ ফ্রিকোয়েন্সি বা ওয়েটের উপর ভিত্তি করে ক্যারেক্টারকে কোড অ্যাসাইন করে যাতে কোডের দৈর্ঘ্য সংশ্লিষ্ট ক্যারেক্টারটির ওয়েটের ওপর ডিপেন্ড করে। হাফম্যান কোড ভেরিয়েবল-লেঞ্জ এবং কোনো প্রিফিক্স ছাড়া (অর্থাৎ কোনো কোড অন্য কোনো কোডের প্রিফিক্স নয়)। যেকোনো প্রিফিক্স-ফ্রি বাইনারি কোডকে একটি বাইনারি ট্রি হিসেবে ডিসপ্লে বা ভিজ্যুয়ালাইজ করা যায় যেখানে এনকোডেড ক্যারেক্টারগুলো লীফে সংরক্ষিত থাকে।

হাফম্যান ট্রি বা হাফম্যান কোডিং ট্রি ডিফাইন করা হয় একটি ফুল বাইনারি ট্রি হিসেবে যেখানে ট্রির প্রতিটি লীফ দেয়া অ্যালফাবেটের একটি লেটারের সাথে কোরেসপন্ড করে।

হাফম্যান ট্রিকে বাইনারি ট্রি হিসেবে বিবেচনা করা হয় যা মিনিমাম এক্সটার্নাল পাথ ওয়েটের সাথে অ্যাসোসিয়েটেড, অর্থাৎ দেয়া লীফ সেটের জন্য ওয়েটেড পাথ লেন্থের মিনিমাম যোগফলের সাথে অ্যাসোসিয়েটেড। তাই লক্ষ্য হলো মিনিমাম এক্সটার্নাল পাথ ওয়েট সহ একটি ট্রি কনস্ট্রাক্ট করা।

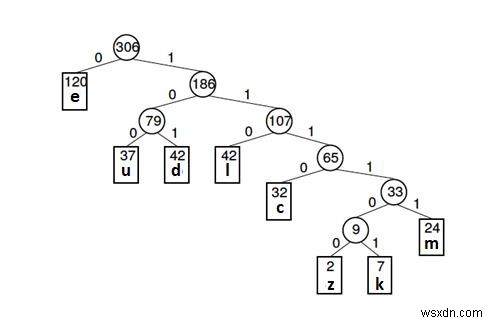
নিচে একটি উদাহরণ দেওয়া হলো -

লেটার ফ্রিকোয়েন্সি টেবিল

হাফম্যান কোড

উপরের উদাহরণের জন্য হাফম্যান ট্রি নিচে দেওয়া হলো -