ডেটা স্ট্রাকচারে B+ ট্রি সন্নিবেশ

এখানে আমরা দেখব, কিভাবে একটি B+ ট্রিতে সন্নিবেশ করা যায়। ধরুন আমাদের নিচের মত একটি B+ গাছ আছে −

B+ গাছের উদাহরণ −

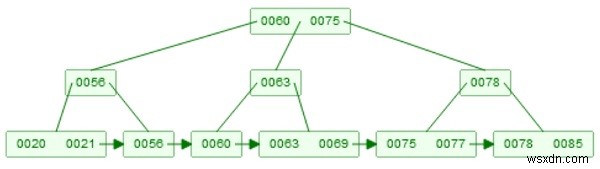
একটি উপাদান সন্নিবেশ করার জন্য, ধারণাটি বি-ট্রির মতোই, যদি একটি উপাদান ঢোকানো হয় তবে সেটি লিফ নোডে সংরক্ষণ করা হবে। যদি এটি কিছু অভ্যন্তরীণ নোডে উপস্থিত থাকে, তবে এটি নিজের সঠিক সন্তান হিসাবে পাতায়ও থাকবে৷

ধরুন আমরা গাছে 65 সন্নিবেশ করতে চাই। তাহলে সেটি 60-এর বেশি এবং 75-এর কম। তারপর এটি মধ্যবর্তী সাব-ট্রিতে ঢোকানো হবে। এখন, 65, 63 এর পরে নোডে ঢোকানো হবে, তারপর সেই নোডটি দুটি ভাগে বিভক্ত হবে, 65 উপরে যাবে এবং 65টিও এর ডান নোডে থাকবে।

65 সন্নিবেশ করার পরে B+ ট্রি।

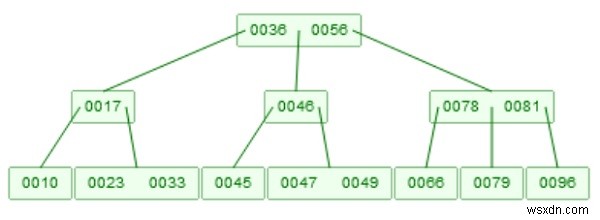
অ্যালগরিদম

BPlusTreeInsert(root, key) −

ইনপুট৷ − গাছের মূল, এবং সন্নিবেশ করার চাবি

We will assume, that the key is not present into the list
Start from root node, perform exact match for key as ‘key’ till a leaf node. Let the search path
be x1, x2, … , xh. The x1 is first node so root, then xh is leaf node. Each node xi is parent of xi+1
Insert the new object where key is ‘key’, and value is v into xh.
i := h
while xi overflows, do
   divide xi into two nodes, by moving the larger half of the keys into a new node p.
   if xi is leaf node, link p into the linked list among leaf nodes.
   identify a key k, to be inserted into the parent level along with child pointer pointing p.
   The choice of k depends on the type of the node xi. If xi is leaf node, we will perform
   copy up. So smallest key in p, is copied as k to the parent level. On the other hand, if xi is
   non-leaf node, then we will perform push up. So smallest key in p, will be copied into k,
   in the parent node.
   if i = 0, then
      create a new index node as the new root. In the new root store node with key k,
      and two child xi and p.
      return
   else
      insert a key k and a child pointer pointing to p, into node xi-1.
      i := i – 1
   end if
done