ভার্চুয়াল ট্রিতে, কিছু প্রান্তকে কঠিন হিসাবে বিবেচনা করা হয় এবং কিছুকে ড্যাশ হিসাবে বিবেচনা করা হয়। সাধারণ স্প্লেয়িং শুধুমাত্র কঠিন গাছে সঞ্চালিত হয়। ভার্চুয়াল ট্রিতে একটি নোড y এ খেলার জন্য, নিম্নলিখিত পদ্ধতিটি প্রয়োগ করা হয়৷
অ্যালগরিদম গাছটিকে তিনবার দেখে, প্রতিটি পাসে একবার, এবং এটি পরিবর্তন করে। প্রথম পাসে, শুধুমাত্র কঠিন গাছগুলিতে স্প্লে করে, নোড y থেকে শুরু করে, y থেকে সামগ্রিক গাছের মূল পর্যন্ত পথটি ড্যাশ হয়ে যায়। এই পথ splicing দ্বারা কঠিন তৈরি করা হয়. নোড y-এ একটি চূড়ান্ত স্প্লে এখন y গাছের মূল তৈরি করবে। কম অনানুষ্ঠানিকভাবে, অ্যালগরিদমটি নিম্নরূপ ব্যাখ্যা করা হয়েছে
Splay(y) এর জন্য অ্যালগরিদম
পাস 1 ভার্চুয়াল গাছে হাঁটুন, কিন্তু স্প্লেয়িং শুধুমাত্র কঠিন উপ-বৃক্ষের মধ্যেই সঞ্চালিত হয়। এই পাসের শেষে, y থেকে রুট পর্যন্ত পথটি ড্যাশ হয়ে যায়।
পাস 2 ওয়াক আপ নোড y থেকে, y এর প্রতিটি সঠিক পূর্বপুরুষকে বিভক্ত করে। এই ধাপের শেষে, y থেকে মূলের পথটি শক্ত হয়ে যায়। তা ব্যতীত, নোড y এবং মূল গাছের সমস্ত শিশু (পাস 1 এর আগে) এখন বাম শিশু হয়ে যায়।
3 পাস নোড y থেকে রুট পর্যন্ত হাঁটুন, স্বাভাবিক ফ্যাশনে খেলুন।
এটি আমাদের সম্ভাব্যতা অনুমান উন্নত করতে পূর্বের জ্ঞান ব্যবহার করতে দেয়। পাতার প্রদত্ত সেটের জন্য। তাই লক্ষ্য হল ন্যূনতম বাহ্যিক পথের ওজন সহ একটি গাছ তৈরি করা।
নিচে একটি উদাহরণ দেওয়া হল
অক্ষর ফ্রিকোয়েন্সি টেবিল
| চিঠি | z | k | m | c | u | d | l | e |
| ফ্রিকোয়েন্সি | 2 | 7 | 24 | 32 | 37 | 42 | 42 | 120 |
হাফম্যান কোড
| চিঠি | ফ্রিকোয়েন্সি | কোড | বিটস |
|---|---|---|---|
| e | 120 | 0 | 1 |
| d | 42 | 101 | 3 |
| l | 42 | 110 | 3 |
| u | 37 | 37100 | 3 |
| c | 32 | 1110 | 4 |
| m | 24 | 11111 | 5 |
| k | 7 | 111101 | 6 |
| z | 2 | 111100 | 6 |
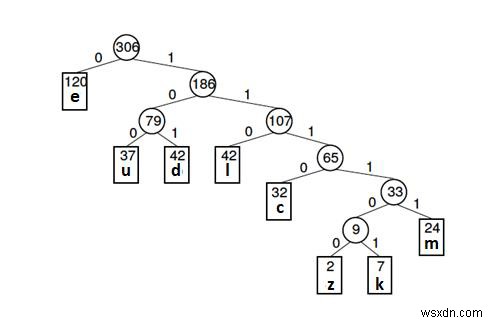
হাফম্যান গাছ (উপরের উদাহরণের জন্য) নীচে দেওয়া হল