মৌলিক ধারণা
একটি বাইনারি গাছকে একটি গাছ হিসাবে সংজ্ঞায়িত করা হয় যেখানে কোনও নোডে দুটির বেশি সন্তান থাকতে পারে না। যেকোনো নোডের সর্বোচ্চ ডিগ্রি হল দুটি। এটি নির্দেশ করে যে একটি বাইনারি গাছের ডিগ্রি হয় শূন্য বা এক বা দুটি।
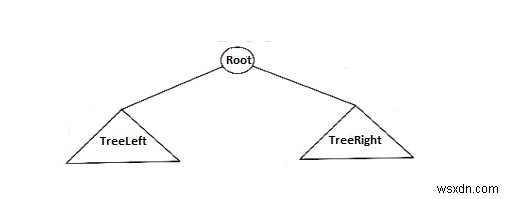
উপরের চিত্রে, বাইনারি গাছে একটি রুট এবং দুটি সাব ট্রি ট্রিলেফ্ট এবং ট্রিরাইট রয়েছে। বাইনারি গাছের বাম দিকের সমস্ত নোডকে বাম সাবট্রি হিসাবে চিহ্নিত করা হয় এবং বাইনারি গাছের ডানদিকের সমস্ত নোডকে ডান সাবট্রি হিসাবে উল্লেখ করা হয়৷
বাস্তবায়ন
একটি বাইনারি গাছে সর্বাধিক দুটি সন্তান থাকে; আমরা তাদের সরাসরি পয়েন্টার বরাদ্দ করতে পারেন. ট্রি নোডের ঘোষণাটি দ্বিগুণ লিঙ্কযুক্ত তালিকার কাঠামোর মতোই, এতে একটি নোড হল একটি কাঠামো যার মধ্যে মূল তথ্য এবং অন্যান্য নোডের দুটি পয়েন্টার (বাম এবং ডান) রয়েছে৷
বাইনারী ট্রি নোড ঘোষণা
typedef struct tree_node *tree_ptr;
struct tree_node
{
element_type element1;
tree_ptr left1; tree_ptr right1;
};
typedef tree_ptr TREE; বাইনারী গাছের প্রকারগুলি
কঠোরভাবে বাইনারি গাছ
কঠোরভাবে বাইনারি গাছ একটি বাইনারি গাছ হিসাবে সংজ্ঞায়িত করা হয় যেখানে সমস্ত নোডের হয় শূন্য বা দুটি সন্তান থাকবে। এটি কোনো নোডে একটি শিশুকে অন্তর্ভুক্ত করে না৷
৷Skew গাছ
একটি তির্যক গাছ একটি বাইনারি গাছ হিসাবে সংজ্ঞায়িত করা হয় যেখানে পাতা ছাড়া প্রতিটি নোডে শুধুমাত্র একটি চাইল্ড নোড থাকে। তির্যক গাছ দুই প্রকার, যেমন বাম তির্যক বাইনারি ট্রি এবং ডান স্ক্যুড বাইনারি ট্রি।
বাম দিকের তির্যক বাইনারি গাছ
একটি বাম তির্যক গাছ শুধুমাত্র বাম সন্তানের সাথে যুক্ত নোড আছে। এটি একটি বাইনারি গাছে শুধুমাত্র বাম উপবৃক্ষ রয়েছে।
ডান তির্যক বাইনারি গাছ
একটি ডান তির্যক গাছ শুধুমাত্র ডান সন্তানের সাথে যুক্ত নোড আছে। এটি একটি বাইনারি গাছে শুধুমাত্র ডান উপবৃক্ষ রয়েছে।
সম্পূর্ণ বাইনারি গাছ বা সঠিক বাইনারি গাছ
একটি বাইনারি গাছকে একটি পূর্ণ বাইনারি গাছ হিসাবে সংজ্ঞায়িত করা হয় যদি সমস্ত পাতা একই স্তরে থাকে এবং প্রতিটি নন-লিফ নোডের ঠিক দুটি সন্তান থাকে এবং এতে সমস্ত স্তরে সর্বাধিক সম্ভাব্য সংখ্যক নোড থাকা উচিত। h উচ্চতার একটি সম্পূর্ণ বাইনারি গাছের সর্বোচ্চ 2h+1 – 1 নোড থাকে।
সম্পূর্ণ বাইনারি গাছ
প্রতিটি নন-লিফ নোডের ঠিক দুটি সন্তান রয়েছে তবে সমস্ত পাতা একই স্তরে থাকা আবশ্যক নয়। একটি সম্পূর্ণ বাইনারি ট্রিকে এমন একটি হিসাবে সংজ্ঞায়িত করা হয় যেখানে শেষ স্তরটি ছাড়া সমস্ত স্তরে সর্বাধিক সংখ্যক নোড থাকে। শেষ স্তরের উপাদানগুলি বাম থেকে ডান দিকে পূর্ণ করা উচিত।
প্রায় সম্পূর্ণ বাইনারি গাছ
একটি প্রায় সম্পূর্ণ বাইনারি গাছকে একটি গাছ হিসাবে সংজ্ঞায়িত করা হয় যেখানে প্রতিটি নোডের একটি ডান সন্তানেরও একটি বাম সন্তান রয়েছে। একটি বাম সন্তান থাকার জন্য একটি ডান সন্তানের জন্য একটি নোড প্রয়োজন হয় না
সাধারণ গাছ এবং বাইনারি ট্রির মধ্যে পার্থক্য
সাধারণ গাছ
- সাধারণ গাছের সন্তানের সংখ্যার কোন সীমা নেই।
- সাধারণ গাছে যেকোনো অভিব্যক্তির মূল্যায়ন করা কঠিন।
বাইনারি ট্রি
- একটি বাইনারি গাছে সর্বাধিক দুটি সন্তান থাকে
- বাইনারি ট্রিতে অভিব্যক্তির মূল্যায়ন সহজ।
গাছের প্রয়োগ
- পাটিগণিত প্রকাশের হেরফের
- প্রতীক টেবিল নির্মাণ
- সিনট্যাক্সের বিশ্লেষণ
- ব্যাকরণ লেখা
- এক্সপ্রেশন ট্রি তৈরি


