পাইথনে একটি বাইনারি অনুসন্ধান গাছের সর্বনিম্ন সাধারণ পূর্বপুরুষ

ধরুন আমাদের একটি বাইনারি সার্চ ট্রি আছে। আমাদের দুটি প্রদত্ত নোডের সর্বনিম্ন সাধারণ পূর্বপুরুষ নোড খুঁজে বের করতে হবে। দুটি নোড p এবং q এর LCA প্রকৃতপক্ষে গাছের সর্বনিম্ন নোড হিসাবে যেখানে p এবং q উভয়ই decedent হিসাবে রয়েছে। সুতরাং যদি বাইনারি গাছটি [6, 2, 8, 0, 4, 7, 9, নাল, নাল, 3, 5] এর মতো হয়। গাছটি −

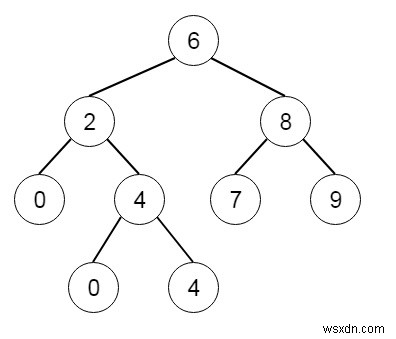
এখানে 2 এবং 8 এর LCA হল 6

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• যদি গাছটি খালি থাকে, তাহলে শূন্য ফেরত দিন
• যদি p এবং q উভয়ই রুট হিসাবে একই হয়, তাহলে রুট ফেরত দিন
• left :=p এবং q ব্যবহার করে রুটের বাম সাবট্রির LCA
• ডান :=p এবং q ব্যবহার করে রুটের ডান সাবট্রির LCA
• যদি বাম এবং ডান উভয়ই অ-শূন্য হয়, তাহলে রুট রিটার্ন করুন
• বাম বা ডানে ফিরুন

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.data = data
      self.left = left
      self.right = right
class Solution():
   def lowestCommonAncestor(self, root, p, q):
      if not root:
         return None
      if p == root or q==root:
         return root
      left = self.lowestCommonAncestor(root.left, p, q)
      right = self.lowestCommonAncestor(root.right, p, q)
      if left and right:
         return root
      return left or right
def insert(temp,data):
   que = []
   que.append(temp)
   while (len(que)):
      temp = que[0]
      que.pop(0)
      if (not temp.left):
         temp.left = TreeNode(data)
         break
      else:
         que.append(temp.left)
      if (not temp.right):
         temp.right = TreeNode(data)
         break
      else:
         que.append(temp.right)
def make_tree(elements):
   Tree = TreeNode(elements[0])
   for element in elements[1:]:
      insert(Tree, element)
   return Tree
def search_node(root, element):
   if (root == None):
      return None
   if (root.data == element):
      return root
   res1 = search_node(root.left, element)
   if res1:
      return res1
   res2 = search_node(root.right, element)
   return res2

root = make_tree([6,2,8,0,4,7,9,None,None,3,5])
ob1 = Solution()
op = ob1.lowestCommonAncestor(root, search_node(root, 2), search_node(root, 8))
print(op.data)

ইনপুট

[6,2,8,0,4,7,9,null,null,3,5]
2
8

আউটপুট

6