একটি প্রদত্ত বাইনারি গাছ পাইথনের লাল-কালো গাছের মতো উচ্চতা ভারসাম্যপূর্ণ কিনা তা পরীক্ষা করুন

ধরুন একটি লাল-কালো গাছ আছে, এখানে একটি নোডের বৃহত্তম উচ্চতা সর্বনিম্ন উচ্চতার দ্বিগুণ। যদি আমাদের একটি বাইনারি অনুসন্ধান গাছ থাকে, তাহলে আমাদের নিম্নলিখিত সম্পত্তি পরীক্ষা করতে হবে। প্রতিটি নোডের ক্ষেত্রে, দীর্ঘতম পাতা থেকে নোড পথের দৈর্ঘ্য নোড থেকে পাতা পর্যন্ত সংক্ষিপ্ততম পথে নোডের দ্বিগুণের বেশি নয়।

সুতরাং, যদি ইনপুট মত হয়

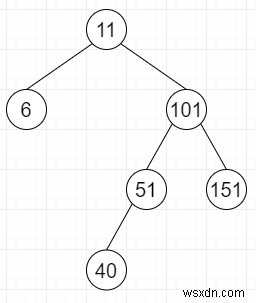
তাহলে আউটপুট হবে True, কারণ এটি ভারসাম্যপূর্ণ।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• একটি ফাংশন সংজ্ঞায়িত করুন solve()। এটি রুট, max_height, min_height
নেবে
• যদি রুট নাল হয়, তাহলে
  • সর্বোচ্চ_উচ্চতা :=0, মিনিট_উচ্চতা :=0
  • সত্য ফেরান
• left_max :=0, left_min :=0
• right_max :=0, right_min :=0
• যদি সমাধান (root.left, left_max, left_min) False এর মত হয়, তাহলে
  • মিথ্যে ফেরত দিন
• যদি সমাধান (root.right, right_max, right_min) False এর মত হয়, তাহলে
  • মিথ্যে ফেরত দিন
• সর্বোচ্চ_উচ্চতা :=সর্বোচ্চ বাম_সর্বোচ্চ এবং ডান_সর্বোচ্চ + 1
• min_height :=সর্বনিম্ন বাম_মিন এবং ডান_মিন + 1
• যদি সর্বোচ্চ_উচ্চতা <=2 * মিনিট_উচ্চতা হয়, তাহলে
  • সত্য ফেরান
• মিথ্যে ফেরত দিন
• প্রধান পদ্ধতি থেকে নিম্নলিখিতগুলি করুন -
• সর্বোচ্চ_উচ্চতা :=0, মিনিট_উচ্চতা :=0
• রিটার্ন সলভ (রুট, সর্বোচ্চ_উচ্চতা, মিন_উচ্চতা)

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

class TreeNode:
   def __init__(self, key):
      self.data = key
      self.left = None
      self.right = None
def solve(root, max_height, min_height) :
   if (root == None) :
      max_height = min_height = 0
      return True
   left_max=0
   left_min=0
   right_max, right_min=0,0
   if (solve(root.left, left_max, left_min) == False) :
      return False
   if (solve(root.right, right_max, right_min) == False) :
      return False
   max_height = max(left_max, right_max) + 1
   min_height = min(left_min, right_min) + 1
   if (max_height <= 2 * min_height) :
      return True
   return False
def is_tree_balanced(root) :
   max_height, min_height = 0,0
   return solve(root, max_height, min_height)
root = TreeNode(10)
root.left = TreeNode(5)
root.right = TreeNode(100)
root.right.left = TreeNode(50)
root.right.right = TreeNode(150)
root.right.left.left = TreeNode(40)
print(is_tree_balanced(root))

ইনপুট

root = TreeNode(10)
root.left = TreeNode(5)
root.right = TreeNode(100)
root.right.left = TreeNode(50)
root.right.right = TreeNode(150)
root.right.left.left = TreeNode(40)

আউটপুট

True