একটি বাইনারি ট্রি দেওয়া হয়েছে, কাজটি হল এটি একটি সম্পূর্ণ বাইনারি গাছ কিনা তা পরীক্ষা করা। প্রতিটি নোডে শূন্য বা দুটি সন্তান থাকলে একটি বাইনারি ট্রিকে সম্পূর্ণ বাইনারি ট্রি বলা হয়।
উদাহরণস্বরূপ
ইনপুট-1

আউটপুট:
1
ব্যাখ্যা: লিফ নোড ব্যতীত প্রতিটি নোডে দুটি সন্তান রয়েছে, তাই এটি একটি সম্পূর্ণ বাইনারি গাছ৷
ইনপুট-2:
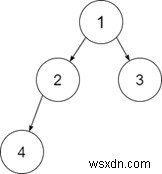
আউটপুট:
0
ব্যাখ্যা: নোড 2 এর শুধুমাত্র একটি সন্তান আছে, তাই এটি একটি সম্পূর্ণ বাইনারি গাছ নয়।
এই সমস্যা সমাধানের পদ্ধতি
একটি প্রদত্ত বাইনারি গাছ পূর্ণ কিনা তা পরীক্ষা করার জন্য, আমরা বাম সাবট্রি এবং ডান সাবট্রির জন্য পুনরাবৃত্তিমূলকভাবে পরীক্ষা করতে পারি।
- নোড এবং তার সন্তান সম্বলিত একটি প্রদত্ত বাইনারি ট্রি ইনপুট করুন৷
- একটি বুলিয়ান ফাংশন হল ফুলবাইনারি ট্রি(নোড*রুট) রুট নোডকে ইনপুট হিসাবে নেয় এবং পূর্ণ বাইনারি ট্রি হলে True ফেরত দেয়, অন্যথায় মিথ্যা।
- বেস কন্ডিশনে, যদি রুট নোডটি NULL বা খালি হয়, তাহলে True রিটার্ন করুন।
- যদি বাম সাবট্রি এবং ডান সাবট্রি শূন্য বা খালি হয়, তাহলে ট্রু রিটার্ন করুন।
- এখন আসুন প্রতিটি বাম সাবট্রি এবং ডান সাবট্রির জন্য বারবার পরীক্ষা করি এবং আউটপুট ফেরত দেই।
উদাহরণ
#include<iostream>
using namespace std;
struct treenode {
int data;
treenode * left;
treenode * right;
};
struct treenode * createNode(int d) {
struct treenode * root = new treenode;
root -> data = d;
root -> left = NULL;
root -> right = NULL;
return root;
}
bool isFullBinaryTree(struct treenode * root) {
if (root == NULL) {
return true;
}
if (root -> left == NULL and root -> right == NULL) {
return true;
} else if (root -> left and root -> right) {
return (isFullBinaryTree(root -> left) and isFullBinaryTree(root -> right));
}
return false;
}
int main() {
struct treenode * root = NULL;
root = createNode(1);
root -> left = createNode(2);
root -> right = createNode(3);
root -> left -> right = createNode(4);
root -> left -> left = createNode(5);
root -> right -> left = createNode(6);
if (isFullBinaryTree(root)) {
cout << "1" << endl;
} else {
cout << "0" << endl;
}
return 0;
} উপরের কোডটি চালানোর ফলে আউটপুট তৈরি হবে,
আউটপুট
0
ব্যাখ্যা: যেহেতু প্রদত্ত বাইনারি গাছের সমস্ত পাতার নোডগুলিতে শিশু নোড নেই, তাই এটি একটি সম্পূর্ণ বাইনারি গাছ নয়। সুতরাং, আমরা 0 হিসাবে আউটপুট পাই।


