পাইথনে একটি প্রদত্ত বাইনারি ট্রিতে সবচেয়ে বড় পারফেক্ট সাবট্রি খুঁজুন

ধরুন আমাদের একটি প্রদত্ত বাইনারি ট্রি আছে; প্রদত্ত বাইনারি ট্রিতে আমাদের সবচেয়ে বড় পারফেক্ট সাব-ট্রির আকার খুঁজে বের করতে হবে। যেমনটি আমরা জানি নিখুঁত বাইনারি গাছ হল একটি বাইনারি গাছ যেখানে সমস্ত অভ্যন্তরীণ নোডের দুটি সন্তান থাকে এবং সমস্ত পাতা একই স্তরে থাকে৷

সুতরাং, যদি ইনপুট মত হয়

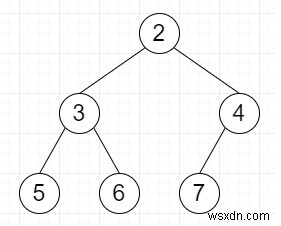
তাহলে আউটপুট হবে 3, এবং সাবট্রি হল

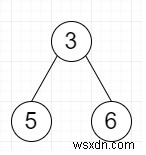
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• RetType নামে একটি ব্লক সংজ্ঞায়িত করুন, এতে isPerfect, উচ্চতা এবং রুটট্রি থাকবে, এগুলি প্রাথমিকভাবে 0

• get_prefect_subtree() নামে একটি ফাংশন সংজ্ঞায়িত করুন, এটি রুট নেয়

• r_type :=একটি নতুন RetType

• রুট যদি None এর মত হয়, তাহলে

  • r_type.isPerfect :=সত্য

  • r_type.height :=0

  • r_type.rootTree :=শূন্য

  • রিটার্ন r_type

• left_subtree :=get_prefect_subtree(root.left)

• right_subtree :=get_prefect_subtree(root.right)

• যদি left_subtree হয় নিখুঁত এবং right_subtree হয় নিখুঁত এবং left_subtree এর উচ্চতা right_subtree এর উচ্চতার সমান হয়, তাহলে

  • r_type এর উচ্চতা :=Left_subtree + 1

    এর উচ্চতা

  • সেট r_type নিখুঁত

  • r_type.rootTree :=রুট

  • রিটার্ন r_type

• সেট r_type নিখুঁত নয়

• r_type.height :=বাম_সাবট্রির সর্বোচ্চ উচ্চতা, ডান_সাবট্রির উচ্চতা

• যদি Left_subtree এর উচ্চতা> right_subtree এর উচ্চতা, তাহলে

  • r_type.rootTree :=left_subtree.rootTree

• অন্যথায়,

  • r_type.rootTree :=right_subtree.rootTree

• রিটার্ন r_type

উদাহরণ

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.data = data
      self.left = left
      self.right = right
def print_tree(root):
   if root is not None:
      print_tree(root.left)
      print(root.data, end = ', ')
      print_tree(root.right)
class RetType:
   def __init__(self):
      isPerfect = 0
      height = 0
      rootTree = 0
def get_prefect_subtree(root):
   r_type = RetType()
   if (root == None) :
      r_type.isPerfect = True
      r_type.height = 0
      r_type.rootTree = None
      return r_type
   left_subtree = get_prefect_subtree(root.left)
   right_subtree = get_prefect_subtree(root.right)
   if (left_subtree.isPerfect and right_subtree.isPerfect and left_subtree.height == right_subtree.height) :
      r_type.height = left_subtree.height + 1
      r_type.isPerfect = True
      r_type.rootTree = root
      return r_type
   r_type.isPerfect = False
   r_type.height = max(left_subtree.height, right_subtree.height)
   if (left_subtree.height > right_subtree.height ):
      r_type.rootTree = left_subtree.rootTree
   else :
      r_type.rootTree = right_subtree.rootTree
   return r_type

root = TreeNode(2)
root.left = TreeNode(3)
root.right = TreeNode(4)
root.left.left = TreeNode(5)
root.left.right = TreeNode(6)
root.right.left = TreeNode(7)

res = get_prefect_subtree(root)
h = res.height

print ("Size: " , pow(2, h) - 1)
print ("Tree: ", end = " ")
print_tree(res.rootTree)

ইনপুট

root = TreeNode(2)
root.left = TreeNode(3)
root.right = TreeNode(4)
root.left.left = TreeNode(5)
root.left.right = TreeNode(6)
root.right.left = TreeNode(7)

আউটপুট

Size: 3
Tree: 5, 3, 6,