পাইথনে একটি প্রদত্ত গাছ থেকে বৃহত্তম বাইনারি অনুসন্ধান সাবট্রি খোঁজার প্রোগ্রাম

ধরুন আমাদের একটি বাইনারি ট্রি আছে, আমাদেরকে বাইনারি সার্চ ট্রি হিসাবে সবচেয়ে বড় সাবট্রি (সর্বোচ্চ সংখ্যক নোড সহ) খুঁজে বের করতে হবে।

সুতরাং, যদি ইনপুট মত হয়

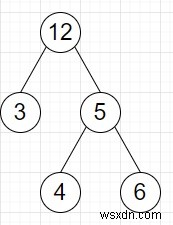
তাহলে আউটপুট হবে

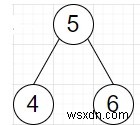
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• সর্বোচ্চ_সাইজ :=[0]
• max_node :=[null]
• একটি ফাংশন ট্রাভার্স () সংজ্ঞায়িত করুন। এটি নোড গ্রহণ করবে
• যদি নোড নাল হয়, তাহলে
  • রিটার্ন নাল
• বাম :=ট্র্যাভার্স (নোডের বামে)
• ডান :=ট্রাভার্স (নোডের ডানদিকে)
• lst :=বাম + [নোডের মান] + ডান
• যদি lst সাজানো হয়, তাহলে
  • যদি max_size[0]
  • max_size[0] :=lst এর আকার
  • max_node[0] :=নোড

উদাহরণ (পাইথন)

আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.val = data
      self.left = left
      self.right = right
def print_tree(root):
   if root is not None:
      print_tree(root.left)
      print(root.val, end = ', ')
      print_tree(root.right)
class Solution:
   def solve(self, root):
      max_size = [0]
      max_node = [None]
      def traverse(node):
         if not node:
            return []
      left = traverse(node.left)
      right = traverse(node.right)
      lst = left + [node.val] + right
      if sorted(lst) == lst:
         if max_size[0] < len(lst):
            max_size[0] = len(lst)
            max_node[0] = node
      return lst

   traverse(root)
   return max_node[0]
ob = Solution()
root = TreeNode(12)
root.left = TreeNode(3)
root.right = TreeNode(5)
root.right.left = TreeNode(4)
root.right.right = TreeNode(6)
print_tree(ob.solve(root))

ইনপুট

root = TreeNode(12)
root.left = TreeNode(3)
root.right = TreeNode(5)
root.right.left = TreeNode(4)
root.right.right = TreeNode(6)

আউটপুট

4, 5, 6,