ধরুন আমাদের একটি বাইনারি ট্রি আছে; আমাদের এই বাইনারি ট্রিতে সর্বাধিক সম্পূর্ণ সাব-ট্রির আকার খুঁজে বের করতে হবে। আমরা জানি যে একটি সম্পূর্ণ বাইনারি ট্রি হল একটি বাইনারি ট্রি যদি সমস্ত স্তরগুলি সম্ভবত চূড়ান্ত স্তর ছাড়াই সম্পূর্ণরূপে পূর্ণ হয় এবং চূড়ান্ত স্তরে যতটা সম্ভব সমস্ত কীগুলি থাকে৷
সুতরাং, যদি ইনপুট মত হয়
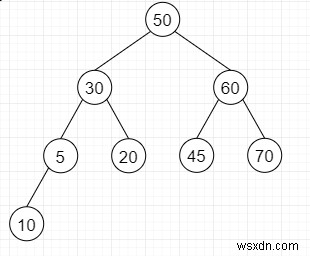
তারপর আউটপুট আকার হিসাবে 4 হবে এবং ইনঅর্ডার ট্রাভার্সাল হবে 10, 45, 60, 70,
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- ইসকমপ্লিট, ইসপারফেক্টের মতো কয়েকটি প্যারামিটার দিয়ে রিটার্নের ধরন সংজ্ঞায়িত করুন, এগুলি প্রাথমিকভাবে মিথ্যা, তারপর আকার এবং রুটট্রি, আকার প্রাথমিকভাবে 0 এবং রুটট্রি শূন্য।
- ret_type :=returnType
- যদি রুট নাল হয়, তাহলে
- ret_type.isPerfect :=সত্য
- ret_type.isComplete :=সত্য
- ret_type.size :=0
- ret_type.rootTree :=কোনটিই নয়
- রিটার্ন_টাইপ
- left_tree :=check Completeness(root.left)
- right_tree :=check Completeness(root.right)
- যদি (left_tree.isPerfect হয় True এবং right_tree.isComplete হয় True এবং বাম ও ডান গাছের উচ্চতা একই হয়, তাহলে
- ret_type.isComplete :=সত্য
- ret_type.isPerfect :=right_tree.isPerfect
- ret_type.size :=left_tree.size + right_tree.size + 1
- ret_type.rootTree :=রুট
- রিটার্ন_টাইপ
- যদি (left_tree.isComplete হয় True এবং right_tree.isPerfect সত্য হয় এবং বাম ও ডান গাছের উচ্চতা একই হয়, তাহলে
- ret_type.isComplete :=সত্য
- ret_type.isPerfect :=মিথ্যা
- ret_type.size :=left_tree.size + right_tree.size + 1
- ret_type.rootTree :=রুট
- রিটার্ন_টাইপ
- ret_type.isPerfect :=মিথ্যা
- ret_type.isComplete :=মিথ্যা
- ret_type.size :=সর্বোচ্চ left_tree.size, right_tree.size
- যদি left_tree.size> right_tree.size, তাহলে
- ret_type.rootTree :=left_tree.rootTree
- অন্যথায়,
- ret_type.rootTree :=right_tree.rootTree
- রিটার্ন_টাইপ
পাইথন
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
import math
class TreeNode:
def __init__(self, data, left = None, right = None):
self.data = data
self.left = left
self.right = right
class returnType :
def __init__(self):
self.isPerfect = None
self.isComplete = None
self.size = 0
self.rootTree = None
def getHeight(size):
return int(math.ceil(math.log(size + 1)/math.log(2)))
def checkCompleteness(root) :
ret_type = returnType()
if (root == None):
ret_type.isPerfect = True
ret_type.isComplete = True
ret_type.size = 0
ret_type.rootTree = None
return ret_type
left_tree = checkCompleteness(root.left)
right_tree = checkCompleteness(root.right)
if (left_tree.isPerfect == True and right_tree.isComplete == True and getHeight(left_tree.size) == getHeight(right_tree.size)) :
ret_type.isComplete = True
ret_type.isPerfect = right_tree.isPerfect
ret_type.size = left_tree.size + right_tree.size + 1
ret_type.rootTree = root
return ret_type
if (left_tree.isComplete == True and right_tree.isPerfect == True and getHeight(left_tree.size) == getHeight(right_tree.size) + 1):
ret_type.isComplete = True
ret_type.isPerfect = False
ret_type.size = left_tree.size + right_tree.size + 1
ret_type.rootTree = root
return ret_type
ret_type.isPerfect = False
ret_type.isComplete = False
ret_type.size =max(left_tree.size, right_tree.size)
if(left_tree.size > right_tree.size ):
ret_type.rootTree = left_tree.rootTree
else:
ret_type.rootTree = right_tree.rootTree
return ret_type
def print_tree(root):
if root is not None:
print_tree(root.left)
print(root.data, end = ', ')
print_tree(root.right)
root = TreeNode(50)
root.left = TreeNode(30)
root.right = TreeNode(60)
root.left.left = TreeNode(5)
root.left.right = TreeNode(20)
root.right.left = TreeNode(45)
root.right.right = TreeNode(70)
root.right.left.left = TreeNode(10)
ans = checkCompleteness(root)
print( "Size:" , ans.size )
print("Inorder Traversal: ", end = '')
print_tree(ans.rootTree) ইনপুট
root = TreeNode(50) root.left = TreeNode(30) root.right = TreeNode(60) root.left.left = TreeNode(5) root.left.right = TreeNode(20) root.right.left = TreeNode(45) root.right.right = TreeNode(70) root.right.left.left = TreeNode(10)
আউটপুট:
Size: 4 Inorder Traversal: 10, 45, 60, 70,


