ধরুন আমাদের একটি বাইনারি গাছ দেওয়া হল। আমাদের গাছ থেকে সবচেয়ে বড় সাবট্রি খুঁজে বের করতে হবে যা বাইনারি সার্চ ট্রি (BST)। আমরা BST এর রুট নোড ফেরত দিই।
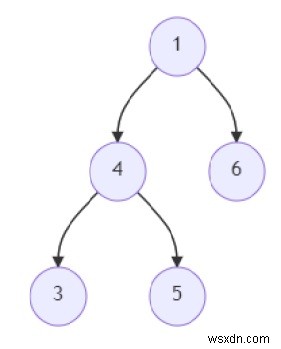
সুতরাং, যদি ইনপুট মত হয়
তাহলে আউটপুট হবে −
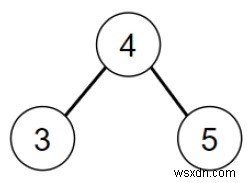
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
- c :=0
- m :=শূন্য
- একটি ফাংশন recurse() সংজ্ঞায়িত করুন। এটি নোড
- নেবে
- যদি নোড নাল না হয়, তাহলে
- left_val :=recurse(নোডের বামে)
- right_val :=recurse (নোডের ডানদিকে)
- গণনা :=ঋণাত্মক অসীম
- যদি (node.left null বা node.left.val <=node.val) এবং (নোডের ডানদিকে null বা node.val <=node.right.val সমান), তাহলে
- গণনা :=left_val + right_val + 1
- যদি গণনা> c, তারপর
- c :=গণনা
- m :=নোড
- রিটার্ন গণনা
- রিটার্ন 0
- যদি নোড নাল না হয়, তাহলে
- রিকারস(রুট)
- রিটার্ন m
উদাহরণ
আরো ভালোভাবে বোঝার জন্য আসুন নিচের বাস্তবায়ন দেখি -
class TreeNode:
def __init__(self, val, left = None, right = None):
self.val = val
self.left = left
self.right = right
def insert(temp,data):
que = []
que.append(temp)
while (len(que)):
temp = que[0]
que.pop(0)
if (not temp.left):
if data is not None:
temp.left = TreeNode(data)
else:
temp.left = TreeNode(0)
break
else:
que.append(temp.left)
if (not temp.right):
if data is not None:
temp.right = TreeNode(data)
else:
temp.right = TreeNode(0)
break
else:
que.append(temp.right)
def make_tree(elements):
Tree= TreeNode(elements[0])
for element in elements[1:]:
insert(Tree, element)
return Tree
def print_tree(root):
if root is not None:
print_tree(root.left)
print(root.val, end = ', ')
print_tree(root.right)
def solve(root):
c, m = 0, None
def recurse(node):
if node:
nonlocal c, m
left_val = recurse(node.left)
right_val = recurse(node.right)
count = -float("inf")
if (node.left == None or node.left.val <= node.val) and (node.right == None or node.val <= node.right.val):
count = left_val + right_val + 1
if count > c:
c = count
m = node
return count
return 0
recurse(root)
return m
tree = make_tree([1, 4, 6, 3, 5])
print_tree(solve(tree)) ইনপুট
tree = make_tree([1, 4, 6, 3, 5]) print_tree(solve(tree))
আউটপুট
3, 4, 5,


