পাইথনের একটি গ্রাফে সমালোচনামূলক এবং ছদ্ম-সমালোচনামূলক প্রান্তগুলি খুঁজে বের করার জন্য প্রোগ্রাম

ধরুন, আমাদের একটি গ্রাফ দেওয়া হয়েছে যাতে 0 থেকে n -1 পর্যন্ত n শীর্ষবিন্দু রয়েছে। গ্রাফটি অনির্দেশিত এবং প্রতিটি প্রান্তের একটি ওজন রয়েছে। সুতরাং গ্রাফটি দেওয়া হলে, আমাদের এমএসটি গ্রাফে সমালোচনামূলক এবং ছদ্ম-সমালোচনামূলক প্রান্তগুলি খুঁজে বের করতে হবে। একটি প্রান্তকে একটি জটিল প্রান্ত বলা হয় যদি সেই প্রান্তটি মুছে ফেলার ফলে MST ওজন বৃদ্ধি পায়। একটি ছদ্ম-সমালোচনামূলক প্রান্ত হল একটি প্রান্ত যা সমস্ত গ্রাফের MST-তে প্রদর্শিত হতে পারে, কিন্তু সব নয়৷ আমরা ইনপুট হিসাবে গ্রাফ দেওয়া প্রান্তের সূচী খুঁজে বের করি।

সুতরাং, যদি ইনপুট মত হয়

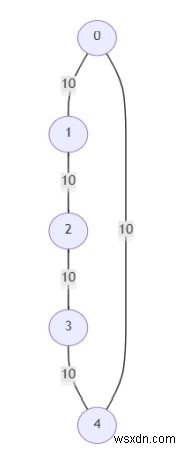
এবং শীর্ষবিন্দুর সংখ্যা হল 5, তাহলে আউটপুট হবে [[], [0, 1, 2, 3, 4]]প্রদত্ত গ্রাফে কোন ক্রিটিকাল এজ নেই এবং সব এজ ছদ্ম-ক্রিটিকাল। যেহেতু সমস্ত প্রান্তের ওজন একই, গ্রাফ থেকে যে কোনো 3টি প্রান্ত একটি MST তৈরি করবে৷

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -

• একটি ফাংশন সংজ্ঞায়িত করুন find_mst()। এটি num_vertices, graph, init :=null, exl :=null

  লাগবে

• একটি সাহায্যকারী ফাংশন পরিদর্শন() সংজ্ঞায়িত করুন। এটি আপনাকে নিয়ে যাবে

• k[u] :=সত্য

• প্রতিটি v, w in graph[u, an empty list], do

  এর জন্য

  • যদি exl এবং u থাকে exl এবং v হয় exl তে, তাহলে

    • পরবর্তী পুনরাবৃত্তির জন্য যান

  • যদি না হয় k[v] সত্য, তাহলে

    • ট্রিপলেট (w,u,v) স্তূপ tmp

      এ পুশ করুন

• res :=0

• k :=False মান ধারণকারী num_array-এর একটি নতুন তালিকা

• tmp :=একটি নতুন গাদা

• যদি init অ-নাল হয়, তাহলে

  • u :=init

  • v :=init

  • w :=init

  • res :=res + w

  • k[u] :=সত্য

  • k[v] :=সত্য

  • ভিজিট(u) বা ভিজিট(v)

• অন্যথায়,

  • ভিজিট করুন(0)

• টিএমপি খালি না থাকার সময়, করুন

  • w :=হিপ টিএমপি

    থেকে সবচেয়ে ছোট আইটেম পপ করুন

  • u :=হিপ টিএমপি

    থেকে সবচেয়ে ছোট আইটেম পপ করুন

  • v :=হিপ টিএমপি

    থেকে সবচেয়ে ছোট আইটেম পপ করুন

  • যদি k[u] এবং k[v] অ-শূন্য হয়, তাহলে

    • পরবর্তী পুনরাবৃত্তির জন্য যান

  • res :=res + w

  • যদি না হয় k[u] সত্য, তাহলে

    • ভিজিট করুন(u)

  • যদি না হয় k[v] সত্য, তাহলে

    • ভিজিট করুন(v)

• k এর সবগুলো সত্য হলে res ফেরত দিন, অন্যথায় ইনফিনিটি ফেরত দিন

• প্রধান পদ্ধতি থেকে, নিম্নলিখিতগুলি করুন:

• গ্রাফ :=প্রদত্ত গ্রাফ

• temp :=find_mst(num_vertices, গ্রাফ)

• c_edge :=একটি নতুন তালিকা

• p_edge :=একটি নতুন তালিকা

• আমি 0 থেকে প্রান্তের মাপ পরিসীমার জন্য, করুন

  • যদি find_mst(num_vertices, graph, exl =edges[i, index 2 to end])> temp, তারপর

    • c_edge

      এর শেষে i ঢোকান

  • অন্যথায়, যদি find_mst(num_vertices, graph, init =edges[i]) temp এর মত হয়, তাহলে

    • p_edge

      এর শেষে i ঢোকান

• [c_edge, p_edge]

  ফেরত দিন

উদাহরণ

আসুন আরও ভালভাবে বোঝার জন্য নিম্নলিখিত বাস্তবায়ন দেখি

from heapq import heappop, heappush
def solve(num_vertices, edges):
   graph = dict()
   for u, v, w in edges:
      graph.setdefault(u, []).append((v, w))
      graph.setdefault(v, []).append((u, w))
   temp = find_mst(num_vertices, graph)
   c_edge, p_edge = [], []
   for i in range(len(edges)):
      if find_mst(num_vertices, graph, exl = edges[i][:2]) > temp:
         c_edge.append(i)
      elif find_mst(num_vertices, graph, init = edges[i]) == temp:
         p_edge.append(i)
   return [c_edge, p_edge]


def find_mst(num_vertices, graph, init = None, exl = None):
   def visit(u):
      k[u] = True
      for v, w in graph.get(u, []):
         if exl and u in exl and v in exl:
            continue
         if not k[v]:
            heappush(tmp, (w, u, v))
   res = 0
   k = [False] * num_vertices
   tmp = []
   if init:
      u, v, w = init
      res += w
      k[u] = k[v] = True
      visit(u) or visit(v)
   else:
      visit(0)

   while tmp:
      w, u, v = heappop(tmp)
      if k[u] and k[v]: continue
      res += w
      if not k[u]:
         visit(u)
      if not k[v]:
         visit(v)
 
   return res if all(k) else inf

print(solve(5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]]))

ইনপুট

5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]]

আউটপুট

[[], [0, 1, 2, 3, 4]]