ধরুন আমাদের n নোড সহ একটি গাছ আছে যা 0 থেকে n-1 পর্যন্ত সংখ্যাযুক্ত। ট্রিটি একটি প্যারেন্ট অ্যারে দ্বারা দেওয়া হয়, যেখানে প্যারেন্ট[i] হল নোড i এর প্যারেন্ট। গাছের মূল হল নোড 0। আমাদের একটি প্রদত্ত নোডের kth পূর্বপুরুষ খুঁজে বের করতে হবে, যদি পূর্বপুরুষ উপস্থিত না থাকে, তাহলে -1 ফেরত দিন
সুতরাং, যদি ইনপুট মত হয়
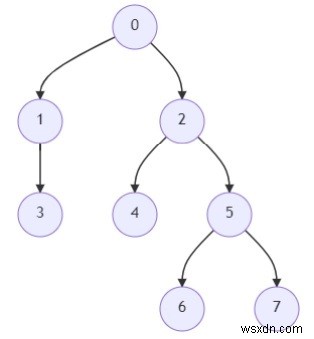
তাহলে আউটপুট হবে 2 কারণ নোড 6 এর প্রথম পূর্বপুরুষ 5 এবং দ্বিতীয়টি 2।
এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব -
-
একটি ফাংশন সংজ্ঞায়িত করুন solve()। এর জন্য প্যারেন্ট, নোড, কে
লাগবে -
যদি নোড -1 এর মত হয়, তাহলে
-
রিটার্ন -1
-
-
অন্যথায় যখন k 1 এর মত হয়, তখন
-
অভিভাবক [নোড]
ফেরত দিন
-
-
অন্যথায় যখন (k এবং k-1) শূন্য হয়, তখন
-
রিটার্ন সলভ(প্যারেন্ট, সলভ(প্যারেন্ট, নোড, k/2 এর ভাগফল), k/2 এর ভাগফল)
-
-
অন্যথায়,
-
msb :=2^(k -1 এর বিটের সংখ্যা)
-
রিটার্ন সল্ভ(প্যারেন্ট, সল্ভ(প্যারেন্ট, নোড, কে-এমএসবি) , এমএসবি)
-
উদাহরণ
আসুন আরও ভালভাবে বোঝার জন্য নিম্নলিখিত বাস্তবায়ন দেখি
def solve(parent, node, k):
if node == -1:
return -1
elif k == 1:
return parent[node]
elif not (k & k-1):
return solve(parent, solve(parent, node, k >> 1), k >> 1)
else:
msb = 1 << (k.bit_length()-1)
return solve(parent, solve(parent, node, k-msb), msb)
parent = [-1,0,0,1,2,2,5,5]
node = 6
k = 2
print(solve(parent, node, k)) ইনপুট
[6,7,9,16,22], 2
আউটপুট
2


