পাইথনে বাইনারি ট্রিতে দ্বিতীয় গভীরতম নোড খুঁজে বের করার প্রোগ্রাম

ধরুন আমাদের একটি বাইনারি গাছ আছে; আমাদের দ্বিতীয় গভীরতম পাতার গভীরতা খুঁজে বের করতে হবে। একাধিক গভীরতম পাতা থাকলে, দ্বিতীয় গভীরতম পাতার নোডটি হবে পরবর্তী সর্বোচ্চ পাতা। আমরা জানি রুটের গভীরতা 0।

সুতরাং, যদি ইনপুট মত হয়

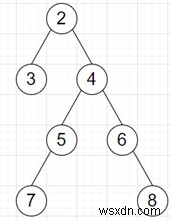
তাহলে আউটপুট হবে 1, যেহেতু দ্বিতীয় গভীরতম নোড হল 3।

এটি সমাধান করতে, আমরা এই পদক্ষেপগুলি অনুসরণ করব:

যদি রুট নাল হয়, তাহলে
- রিটার্ন নাল
নোডস :=একটি নতুন তালিকা
নোডের শেষে রুট ঢোকান
গণনা :=0, আগের :=0, এখন :=0
যখন নোড খালি না থাকে, তখন কর
- নতুন :=একটি নতুন তালিকা
- পতাকা :=সত্য
- নোডের প্রতিটি নোডের জন্য, করুন
  - যদি পতাকা সত্য হয় এবং (নোডের বাম অংশ নাল থাকে) এবং (নোডের ডানদিকে নাল থাকে), তাহলে
    - আগের :=এখন
    - এখন :=গণনা
    - পতাকা :=মিথ্যা
  - নোডের বাম অংশ যদি শূন্য না হয়, তাহলে
    - নতুনের শেষে নোডের বাম দিকে ঢোকান
  - যদি নোডের ডানদিকে শূন্য না হয়, তাহলে
    - নতুনের শেষে নোডের ডানদিকে ঢোকান
- নোডস :=নতুন
- গণনা :=গণনা + 1
আগের রিটার্ন

আরও ভালভাবে বোঝার জন্য আসুন নিম্নলিখিত বাস্তবায়ন দেখি:

উদাহরণ

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.data = data
      self.left = left
      self.right = right

class Solution:
   def solve(self, root):
      if root is None:
         return None
      nodes = []
      nodes.append(root)
      count = 0
      prev = 0
      now = 0
      while nodes:
         new = []
         flag = True
         for node in nodes:
         if flag and (not node.left) and (not node.right):
            prev = now
            now = count
            flag = False
         if node.left:
            new.append(node.left)
         if node.right:
            new.append(node.right)
      nodes = new
      count += 1
   return prev

ob = Solution()
root = TreeNode(2)
root.left = TreeNode(3)
root.right = TreeNode(4)
root.right.left = TreeNode(5)
root.right.right = TreeNode(6)
root.right.left.left = TreeNode(7)
root.right.right.right = TreeNode(8)
print(ob.solve(root))

ইনপুট

root = TreeNode(2)
root.left = TreeNode(3)
root.right = TreeNode(4)
root.right.left = TreeNode(5)
root.right.right = TreeNode(6)root.right.left.left = TreeNode(7)
root.right.right.right = TreeNode(8)